Like an economist at Wimbledon
To what extent is future success affected by past success? This topical question has implications for many areas of society, including education. However, a new study suggests that the answer may come from an unexpected direction: tennis. We look at why tennis players who are matched against someone of similar ability are more likely to win a point if they won the previous one, even if the earlier point was gained by pure chance.
What is the key to success? This question is the subject of many professional development books and business school courses. Traditionally, the debate is seen from one of two views of the world. Some believe that success is primarily a matter of innate talent, determined perhaps by genetics or early childhood development. Others consider that it is primarily a matter of environment and hard work, and that every individual has the opportunity to develop his or her potential if given the chance. This latter line of thought is embodied in the ‘10,000-hour’ rule, which predicts that with 10,000 hours of training, anyone could reach the standard of a professional violinist or tennis player.
The reality is more complex: talent and environment both have an impact, and they are closely linked.
While enjoying Wimbledon this summer, you may wonder what determines success on the court. Perhaps surprisingly, behavioural economics and econometrics can shed some light on the question. As economists Romain Gauriot and Lionel Page found when they analysed large datasets from tennis matches, sometimes the answer is simply success itself!
The momentum from gaining key points
Gauriot and Page studied to what extent winning a point affects subsequent rallies between players.1 They analysed 334,813 points in 3,561 professional tennis matches within major tournaments such as Grand Slams, Masters 1000s, WTA Premiers, Fed Cups and Davis Cups over the period 2005–09. The outcome of each point was logged via Hawk-Eye technology, which is able to record a ball bounce within a margin of error of 0.36cm. As the server benefits from an inherently higher probability of winning a point than the receiver, game points were excluded from the study (i.e. 40–0, 40–15, 40–30, ‘Advantage’). Indeed, analysing such points would bias the results as the identity of the server could change after a game point.
It is difficult to estimate such an effect because of skill discrepancies between tennis players. Indeed, regardless of the outcome of the previous points played between two players, if one player is clearly more skilled than the other, his or her probability of winning the next point will be much higher. To minimise the impact of level discrepancies, the researchers considered only those ball bounces that were located close (less than 6cm) to court lines. This was based on the assumption that players who are able to put balls close to the line are of similar ability.
Figure 1 below shows all the bounce marks in the dataset (in grey) and the male players’ bounce marks (in black) within 6cm of the line that were considered in the analysis. In order to compare points where the players’ ability was not a factor in determining success, the authors restricted the analysis to the black points only.
Figure 1 Bounce marks included in the dataset
Beyond a certain degree of accuracy, however, the ball’s positioning is not determined by the player’s ability, but comes down to luck. Indeed, to take an extreme example, the researchers assume that placing a ball 0.1mm ‘in’ rather than 0.1mm ‘out’ does not result from the intrinsic talent of the player, but mostly from luck. Moreover, both Hawk-Eye technology and referees can make mistakes, so it is possible to win a point by putting a ball slightly ‘out’, or lose one by putting it slightly ‘in’.
This is demonstrated in Figure 2 below, which shows that there is no clear discontinuity at the threshold value zero. This means that a player has a chance of winning a point even if they put one or more balls out during the point. In the same way, the unexpectedly reduced probability of winning a point for a ball that is slightly ‘in’ can be explained by the fact that a ball placed just ‘in’ might be called out by either the referee or the Hawk-Eye technology, which would mean a zero probability of winning the point.
Indeed, a player always benefits from an increased probability of winning the point by placing balls ‘in’ as close as possible to the court lines, as it becomes increasingly difficult for their opponent to return the ball and put them in a difficult position. However, players are exposed to mistakes by the referee or the Hawk-Eye technology that may wrongly judge the ball to be out. In theory, without a margin of error, we should observe a perfect discontinuity around the threshold value (i.e. zero probability of winning the point for bounces out of the court, and a strictly positive probability for all bounces within the boundaries of the court).
In econometrics, it is important to consider causality in order to avoid misinterpreting a relationship between two variables and misunderstanding the effects of one factor on another.2 Consequently, the researchers excluded balls that were very close to the line (within 1cm) to alleviate the potential effect of this discontinuity on the results. A naïve approach here would have been to consider that, if a player places a ball just out, even an infinitesimal distance from the line, they will automatically lose the point.
Figure 2 Probability of winning a point based on ball positioning
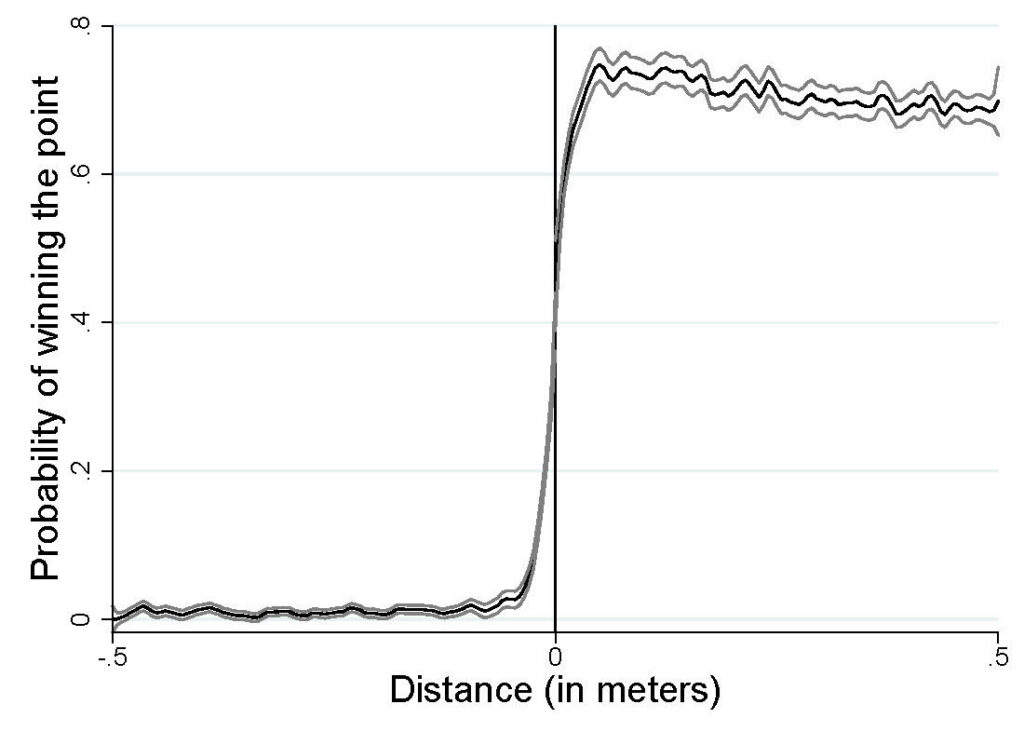
Source: Gauriot, R. and Page, L. (2019), ‘Does Success Breed Success? a Quasi-Experiment on Strategic Momentum in Dynamic Contests’, The Economic Journal, 129:624, pp. 3107–3136. Reproduced with the authors’ permission.
So, what drives this effect?
The strategic effect of success on success
The researchers first turned to game theory3 and the strategic choices made by players. This assumes that players may modulate their efforts depending on the stakes in the game. This theory is explained further in the box below.
A recent example is the 2019 Wimbledon match between Nick Kyrgios and Jordan Thompson where Kyrgios, after winning a tough third set 7/6(10) in 1 hour and 15 minutes, lost the fourth set 6–0 to his opponent in just 18 minutes,4 preferring to keep his concentration and energy for the final set, which he won 6–1. This was also the case in the 2001 French Open match between Marat Safin and Fabrice Santoro, where the latter sacrificed the fourth set 6–0 in order to recover from the effort of playing the previous set, before winning the fifth set 6–1. Asked about his strategy in the press conference following the match, Santoro said, ‘It was risky, but I needed 20–25 minutes of rest. I did not have any energy anymore’.5
Strategic allocation of effort in a best-of-five contest
Alice and her opponent are playing tennis. Their match consists of five sets, and whoever wins three sets wins the match.
Suppose that the outcome of a set depends on (i) skill; (ii) effort; and (iii) luck. In the moments before her match starts, Alice cannot choose how skilful or lucky she is going to be. (Her skill is determined by how well she trained in the preceding weeks and months. Her luck is, by definition, random white noise.)
However, Alice can choose to put more effort or less effort into the match. If Alice believes she has a good chance of winning, she may choose to put effort into each set.
What if Alice has a run of bad luck and loses the first two sets? In this case, her optimal approach might be to conserve her efforts for her next match, which has higher expected returns. Alice will not have wasted her effort if she loses a set (her expected value, conditional on losing a set, is not zero); and she will win the match if she wins three sets.
However, in the current match Alice’s efforts will lead to lower expected returns—and, if these efforts are costly, perhaps even negative returns. She needs to win every subsequent set to win the match. If she loses even a single set, she will have wasted her efforts (her expected value, conditional on losing a set, will be zero).
Therefore, Alice is more likely to have negative expected returns to effort if she has already lost two sets in a match. If this is the case, the strategically rational decision for her is to not invest effort in the match. Instead, she should conserve these efforts to invest in her next match.
The behavioural effects of success
This prediction of a positive effect of success due to strategic decisions is similar to another mechanism whereby the experience of success has an effect on performance via its effect on the player’s mindset and confidence.6
The notion of self-confidence, which often plays a role in psychology, suggests that initial success may change a player’s belief about their relative strength in a contest. Another explanation is that winning a key point can give the winning player a psychological upper hand by putting the losing player under pressure, pushing them to make tactical or technical mistakes. The box below gives an example.
Of lobsters and men
Perhaps the most famous, albeit indirect, reference to the theory of the psychological momentum of success is from a controversial Canadian academic and psychologist, Dr Jordan Peterson.
In his book 12 Rules for Life, Peterson tells a parable of a lobster. When two equally matched lobsters fight and one wins by chance, the winning lobster receives an injection of serotonin.1 This causes it to adopt a more aggressive posture and display a more assertive attitude towards other lobsters,2 and it thereby becomes physically stronger. In other words, having been successful in the past gives the lobster a psychological boost that sets it on a path-dependent trajectory to yet more future successes.
Conversely, the losing lobster becomes dejected, adopts a more submissive posture, displays a less assertive attitude towards other lobsters, and thereby becomes physically weaker. Previous failures will have set this lobster on a path-dependent trajectory to yet more future failures.
It is generally assumed that humans are capable of exercising more free will than lobsters. Peterson’s argument is that people should try to mimic successful people rather than less successful people, in thought, words and posture, even when they are not themselves successful. This could help to launch them onto a trajectory of successes, where each subsequent success becomes easier than the last.
In any event, past victories may have a far-reaching influence on the results of future contests—perhaps with people just as much as with lobsters.
1 Peterson, J. (2018), 12 Rules of Life, Allen Lane. 2 For example, see Huber, R., Smith, K., Delago, A., Isaksson, K. and Kravitz, E.A. (1997), ‘Serotonin and aggressive motivation in crustaceans: altering the decision to retreat’, Proceedings of the National Academy of Sciences, 94, 5939–42.
What are the economic implications?
These examples illustrate how an individual’s performance is correlated with their previous performance over time, and how past success or failure affects future behaviour, even when success is down to luck. Success may not necessarily be due to innate ability or effort, but might be explained by the experience of success itself.
Interestingly, Gauriot and Page did not find a momentum effect among female players. While their study does not allow them to conclude on the ultimate reasons for this, one explanation in the literature is that men tend to favour competitive environments more than women do, and to react differently to incentives in dynamic games.7
The implications of finding a correlation between previous and future performance are important. Consider the workplace, for example. When a managerial model pits employees against each other on a day-to-day basis, it is possible that the initial success of one employee, perhaps achieved by chance, will discourage other team members and lead to less collective effort, which would have a negative effect on individuals and the community.
Gauriot and Page’s data did not allow them to definitively determine the origins of the momentum that they identified. However, if the psychological explanation (which suggests that mental pressure plays a key role) is correct, it may be possible to suppress this effect through mental preparation in order to reduce the significance of past failures.
Indeed, more recent research suggests that this is the case, and that providing detailed information on individual performance and the root causes of success and failure in competitions may help to overcome discouragement effects.8
1 Gauriot, R. and Page, L. (2019), ‘Does Success Breed Success? a Quasi-Experiment on Strategic Momentum in Dynamic Contests’, The Economic Journal, 129:624, pp. 3107–3136.
2 For further details, see Oxera (2021), ‘Causality and natural experiments: the 2021 Nobel Prize in Economic Sciences’, Agenda, November.
3 Game theory studies how economic agents (here, tennis players) make strategic choices based on their respective preferences. It involves modelling the strategic interaction of the players in a situation where rules are clearly defined and outcomes identifiable. See the prisoner’s dilemma example for a well-known game theory problem. Given the fact that tennis matches represent a competitive environment with well-defined rules and outcomes (such as significant stakes or prize money), they are perfectly suited to a game theory approach.
4 This is an unusually short duration, as on average sets last around 40–45 minutes.
5 Translation by Oxera from ‘C’était risqué, mais j’avais besoin de 20–25 minutes de repos, je n’avais plus de force’. Source: Dhers, G. (2001), ‘Contre Safin, Santoro justifie ses moyens’, Liberation, 4 June.
6 For a discussion see, for instance, Descamps, A., Ke, C. and Page, L. (2022), ‘How success breeds success’, Quantitative Economics, 13:1, pp. 355–385.
7 For instance, Niederle and Vesterlund analysed to what extent competitive environment’s approach can be attributed to gender and found that women tend to move away from competition while men tend to embrace it. See Niederle, M. and Vesterlund, L. (2007), ‘Do women shy away from competition? Do men compete too much?’, The Quarterly Journal of Economics, 122:3, pp. 1067–1101.
8 Descamps, A., Ke, C. and Page, L. (2022), ‘How success breeds success’, Quantitative Economics, 13:1, pp. 355–385
Related
Switching tracks: the regulatory implications of Great British Railways—part 2
In this two-part series, we delve into the regulatory implications of rail reform. This reform will bring significant changes to the industry’s structure, including the nationalisation of private passenger train operations and the creation of Great British Railways (GBR)—a vertically integrated body that will manage both track and operations for… Read More
Cost–benefit analyses for public policy
Cost–benefit analyses (CBA) are commonly applied to public infrastructure projects where there is a degree of certainty about the physical output of the project and the consequent societal benefits. CBA can also be applied to proposed policy and regulatory changes, but there is less clarity about the outcomes and the… Read More