Death of an old star…evolution of a new one?
‘Superstar firms’ are increasingly dominating markets. Network effects may consolidate the position of these firms, but they can also help new entrants to undermine them. In some markets, network effects will both dampen competition ‘within’ the market and spur competition ‘for’ the market. Francesca Arduini, Oxera Analyst, argues that we can employ the framework of evolutionary game theory to derive four key policy insights into this topic.
Traditional competition policy focuses on the number of firms in a market and their market shares. This type of competition can be characterised as competition ‘within’ the market. However, it has long been acknowledged that competitive forces operate in a broader way. In some cases, a market may be highly concentrated and yet be very competitive due to the pressure exerted by potential entrants on the incumbent firm(s)—i.e. competition ‘for’ the market.
The interest in competition ‘for’ the market has increased as some empirical studies have found evidence of decreased competition ‘within’ the market, raising alarm bells about the broader competitiveness of world markets.1 An increasing number of markets feature a few very large players; the literature characterises these as ‘winner takes most’ markets, and the incumbent firms in them as ‘superstar firms’.2
Existing tools to assess the degree of competition ‘for’ the market are limited—for instance, there is no consensus on a rigorous way to estimate the probability of entry in a market after a merger. Therefore, if competition for the market is becoming increasingly important relative to competition within the market, it is important to develop new tools so that policy can remain effective. In this context, evolutionary game theory can provide powerful insights when combined with more traditional policy tools.3
Jumping on the bandwagon
In order to model competition ‘for’ the market, it is essential to have a theory about what its main drivers are. This article focuses on positive network externalities to consumption, which occur when the benefit that a consumer receives from a good or service increases with the number of other individuals who choose that good or service. An example of this is fashion: an individual might want to wear bell-bottoms only if others are doing so too.
As described below, evolutionary game theory takes into consideration the ability of individuals to care about the consumption decisions of others, making it a useful framework for analysing the effect of network externalities.
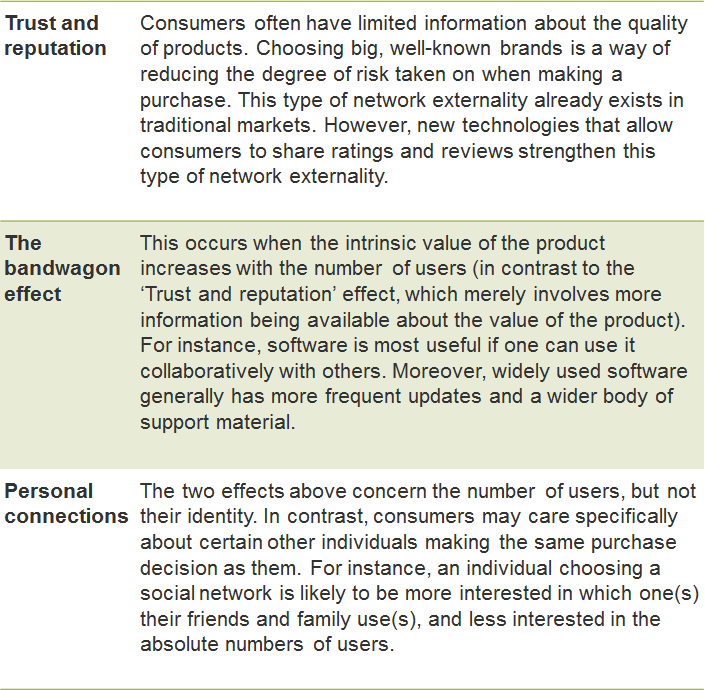
As shown in Table 1, network externalities fall into three broad categories—trust and reputation, the bandwagon effect, and personal connections.
Table 1 Network effects
Evolutionary game theory: a framework
Game theory has become a well-established part of the economist’s toolkit, as it is a powerful way of modelling situations in which individuals make choices that are interrelated—i.e. where the benefit from individual A choosing X depends on individual B’s choice.
However, the standard game theory framework makes very strong assumptions about individuals’ degrees of rationality and knowledge.4 Because of this, the empirical predictions of game theory are more successful in capturing reality in contexts where players are rational and well informed, such as auctions or interactions between firms.
This article focuses on consumer choice as a driver of market dynamics. Given that consumers often do not make choices in a very well-informed or rational manner (as increasingly acknowledged in the field of behavioural economics), it is preferable to employ a game theory framework that makes weaker assumptions about the preferences and cognitive abilities of players. One such framework is evolutionary game theory.5
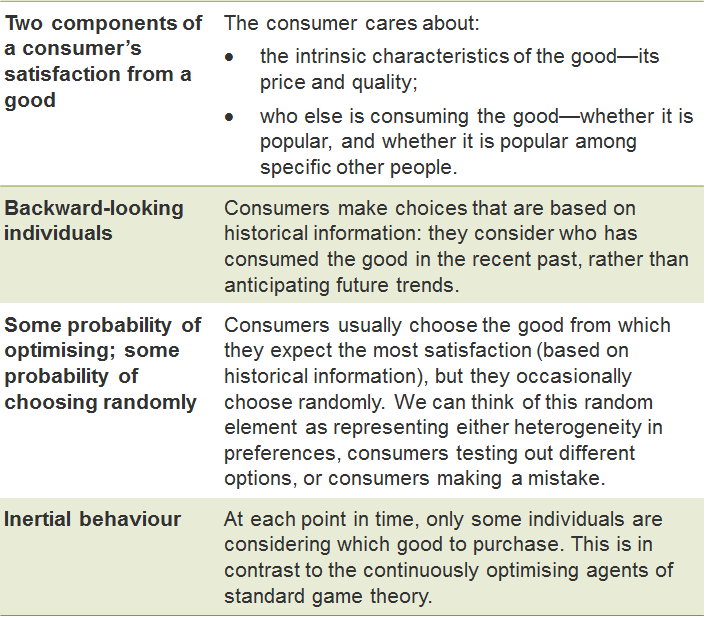
This broader framework encompasses a range of models, many of which display the characteristics illustrated in Table 2.
Table 2 Consumer traits in evolutionary game theory
Long-run market evolution—from hero to zero
Evolutionary game theory yields two key insights into the long-run behaviour of markets with network externalities:
- the market will exhibit ‘punctuated equilibrium’ behaviour;
- in the long run, the market equilibrium is likely to maximise the overall wellbeing of consumers.
What is meant by these concepts? Returning to the example of bell-bottoms, the fashion market features excellent examples of the kind of long-run behaviour we might expect to see in markets with network externalities. At any time, there will be a high degree of uniformity in consumer choice. However, over time, there will be stark changes in the good being consumed (changes in fashion trends). In evolutionary game theory, this is known as ‘punctuated equilibrium’ behaviour.
This behaviour is observed when an equilibrium persists for some time, with small deviations being made due to individuals making mistakes or testing out new options. Given enough time, a large enough group of individuals will simultaneously deviate from that established equilibrium, ‘punctuating’ it. Once the number of individuals leaking out of the punctuated equilibrium reaches a critical mass, the old equilibrium will fully deflate, with the system tipping towards a new equilibrium. This process repeats indefinitely.6
These changes in equilibrium are the incarnation of competition ‘for’ the market. It should be noted that if firms are aware that they might lose consumers to a new entrant, they might seek to pre-empt this by innovating. Therefore, while we may not end up seeing changes in the firms that are present in the market, there can be a healthy underlying competitive pressure for the incumbent firms to innovate, thereby increasing consumer welfare.
To simplify, however, consider a case in which firms cannot innovate—and therefore incumbent firms are eventually replaced by new, better firms. We can extend the insights from this simplified situation to more realistic cases as follows.
- Policy insight I: the frequency with which we expect the equilibrium to change is a measure of the strength of competition ‘for’ the market. This frequency depends on specific market characteristics, as discussed below.
- Policy insight II: competition ‘for’ the market is likely to bring about good outcomes for consumers in the long run, and therefore the lack of competition ‘within’ the market is not sufficient cause for alarm, as long as competition ‘for’ the market exists.
The formal result from evolutionary game theory is that the system is more likely to exhibit Pareto efficient outcomes (such that no consumer can be made better off without another consumer being made worse off) than inefficient ones in the long run. The reasoning for this is as follows. If an outcome is inefficient, multiple consumers will be willing to change their behaviour; given the ‘punctuated equilibrium’ nature of the system, this means that an inefficient situation will be ‘punctuated’ quickly, and that the system will move on to a more efficient outcome. Inefficient outcomes might persist for some time, but they will be less stable than efficient ones. This means that we are less likely to observe them, and if we do, we are likely to observe them for shorter times than efficient outcomes.
However, what constitutes the ‘long run’ is open to interpretation, and the exact time we expect to wait for the efficient outcome to materialise will depend on the specifics of the market. This is discussed in more detail below.
Which markets should we worry about?
From the policymaker’s viewpoint, a market will give more cause for concern if it features fewer changes in equilibrium (weaker competition ‘for’ the market) and if the welfare-maximising long run is further away. An interesting result from evolutionary game theory is that there is not actually a trade-off between these desirable outcomes. Both are affected in the same way by the following two key characteristics of a market: (a) locality of the network; and (b) frequency of random choice.
The locality issue leads to the following policy insight.
- Policy insight III: we should worry most about markets where network effects are global rather than localised. If, for example, consumers care only about their close family’s consumption choices then the network is deemed to be localised. If, instead, they care about the total number of other users, the network is global. This is explained in further detail in the box below.
A simple model of local interaction
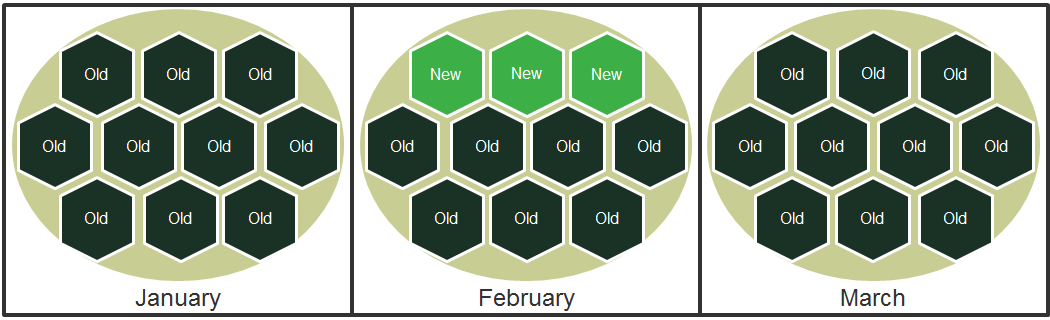
To model network effects, we represent individuals as nodes (hexagons in the figures below) in graphs (diagrams that show the relationship between nodes). In this setting, neighbours (hexagons that share a border in the figures below) are individuals who care about each other’s choices.
For example, consider a market in which all agents are currently buying the same ‘old’ product. A new market entrant produces another ‘new’ product, which has a superior price–quality ratio. Individuals prefer goods that are cheaper and higher quality, but they also care about the proportion of their local group that has already adopted that good. Specifically, the trade-off between these two goods is such that an individual prefers the new product if at least a third of its neighbours have adopted it. To simplify the scenario, we assume that all individuals reconsider their choice each month. They base their choice for next month’s consumption on today’s adoption patterns (backward-looking). Sometimes the choices made are random.
To begin with, nobody adopts. In January, because nobody has adopted yet, each individual prefers not to adopt. Eventually (in February), some individuals mistakenly/randomly adopt the new product anyway. Consider the case of three neighbouring agents making a mistake at the same time (they may all have a related reason for having made a mistake). To explore the impact of the extent of localisation, we consider the following two different network structures.
Figure 1 Highly localised network

In the figure above, the network has a localised structure. This leads to the new, better product completely taking over the market between January and June. Precisely because the new product is better than the old one, once it has a foothold in the market (in February) those same network effects that had hindered it from immediately taking over the market (in January) propel it to conquer the whole market (in March through to June). At that stage, there is a chance that some individuals will randomly switch back to the old product, but because that product has a lower quality–price ratio, it will be difficult for it to overthrow the new product (yielding the result that, in the long run, outcomes are likely to maximise consumer welfare).
Figure 2 Globalised interaction
Source: Arduini, F.
The second figure depicts a totally interconnected network. Because agents care about the product choice of the whole population, a very high number of contemporaneous mistakes is required for there to be a switch in the equilibrium. In our example, only three individuals randomly switch to the new product in February. Because they are connected to all the other individuals, it is optimal for them to switch back to the old product in March because less than one-third of their connections also use the new product. Therefore, even though the new product is better than the old one, it does not gain enough of a foothold to take over the market. Four contemporaneous mistakes are required for an equilibrium switch to occur, and this is significantly less likely to happen than three contemporaneous mistakes. Therefore, the expected time before an equilibrium switch in the second figure is higher than in the first figure, and this happens exclusively because of the different degrees of locality of the network interactions in the two cases.
Source: Arduini, F.
In addition, the frequency of random choice issue leads to the following.
- Policy insight IV: we should worry more about markets where consumer choice is rarely ‘random’. Interpreting what this means in terms of policy prescriptions is not straightforward. This is because there are multiple legitimate interpretations of random choice in evolutionary game theory models—preference heterogeneity, individuals testing out new goods, and individuals being uninformed or making mistakes. The box below discusses the interpretation that is most likely—the ‘hipster effect’.
The ‘hipster effect’
One way of interpreting evolutionary mistakes is to think of consumers trying out new, niche products. We might refer to this as the ‘hipster effect’. Hipsters (or influencers) try out new products; if these individuals like the products, less adventurous individuals also start consuming them, and the product becomes mainstream. An important question then is under what circumstances the ‘hipster effect’ will be strong.
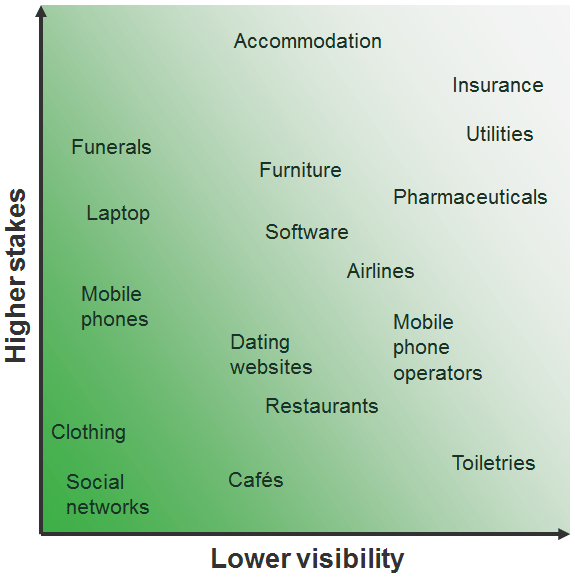
Figure 3 The ‘hipster effect’ is strongest with low stakes and high visibility
Source: Arduini, F.
As illustrated in the figure above, we can expect individuals to test out new products more in markets where products are sufficiently ‘trendy’ and visible, and in which the risk from making a bad choice is lower. For instance, one is likely to experiment with a new café as this is a low-price, one-off choice without grave or long-term effects. On the other hand, one is unlikely to experiment with a new energy supplier as it is not socially prominent and the potential downside can be serious and enduring (such as months without central heating in the winter). By contrast, one is likely to experiment with a new social network, especially as it is possible to do so while also using more established social networks.
Source: Arduini, F.
What are the main policy implications?
Evolutionary game theory provides a powerful toolkit to analyse competition for the market and draw policy recommendations. Lack of competition ‘within’ the market is not sufficient cause for concern, as long as the market has features that indicate strong competitive pressures acting ‘for’ the market.
The intensity of competition for a market can be captured by the frequency with which the equilibrium would switch if the incumbent provided low-value-for-money products relative to potential entrants. However, this is a counterfactual that might not materialise, given that incumbents might innovate in response to competitive pressures. Therefore, policymakers might wish to focus on other market characteristics. In particular, they could scrutinise markets where network effects are less localised and hipster effects are likely to be weak—the software market, for instance, rather than social networks.
However, it must be stressed that competition is multi-faceted, and therefore antitrust policy must also be multi-faceted. New approaches must complement more traditional measures, rather than be a substitute for them.
1 De Loecker, J. and Eeckhout, J. (2018), ‘Global Market Power’, No. w24768, National Bureau of Economic Research, May.
2 Autor, D., Dorn, D., Katz, L.F., Patterson, C. and Van Reenen, J. (2017), ‘The fall of the Labor share and the Rise of Superstar Firms’, MIT Working Paper, 2 May.
3 Arduini, F. (2019), ‘Death of an Old Star… Evolution of a New One’, working paper.
4 Common knowledge of rationality, for instance, is widely recognised as being unrealistic. This is the assumption that there is an infinite regress of ‘player 1 knows that player 2 knows that player 1 … is rational’.
5 Another considerable advantage of evolutionary game theory is that it suffers from fewer equilibrium selection problems than ‘standard’ game theory. Young, H.P. (1998), Individual Strategy and Social Structure: An Evolutionary Theory of Institutions, Princeton University Press.
6 Some markets will exhibit some types of negative network externalities, as well as positive ones. Equilibria might be inherently unstable, because if a product is too widely used it becomes ‘too mainstream’ and some individuals will reject it favour of new products (see more below on the ‘hipster effect’).
Download
Contact

Matthew Johnson
PartnerContributor
Related
- Energy
- Financial Services
- Pharmaceuticals and Life Sciences
- Telecoms, Media and Technology
- Transport
- Water
Download
Related

The role of regulation in spurring innovation and growth in the EU and the UK
Since the 2008 financial crisis, both the EU and the UK have experienced sustained periods of low growth and weak productivity. The COVID-19 pandemic further exacerbated these trends, and their share of global GDP has continued to decline, especially relative to the US and emerging economies. This has provoked scrutiny… Read More

Reasserting the UK’s FRAND framework: implications of the Court of Appeal’s decision in Optis v Apple
Nearly a decade after establishing the UK’s FRAND framework in Unwired Planet v Huawei (2017), Lord Justice Birss returned in Optis v Apple (2025)—this time in the Court of Appeal—to steer the law back to his original approach.1 That means identifying the closest comparator(s), adjusting the… Read More
