Computer move? Chess cheaters and the limits of algorithmic detection
In September 2022, World Chess Champion Magnus Carlsen dramatically quit a tournament after losing a game to teenage Grandmaster Hans Moke Niemann, leading many to accuse Niemann of cheating. Niemann has since launched a court case for slander, libel and unlawful group boycott against Carlsen and other members of the chess community. If this case makes it to trial, it will need to address the question: do cheating detection algorithms accurately identify cheaters?
While Carlsen initially stayed quiet about his reasons for quitting, the chess world quickly concluded that he suspected Niemann of cheating, which would make the incident arguably the largest cheating scandal in chess history. Eventually, Carlsen broke his silence, stating that Niemann had ‘cheated more – and more recently – than he has publicly admitted’.1
A month later, Niemann responded by filing a $100m lawsuit for slander, libel and unlawful group boycott under the Sherman Antitrust Act.2 The Defendants in this case are the online chess website Chess.com, Play Magnus Group, and two further chess players: Grandmaster Hikaru Nakamura, and International Master Danny Rensch (who is also Chess.com’s Chief Chess Officer). If the case is brought to court, the key question will be whether it is possible to prove, on the balance of probabilities, that Niemann cheated in his game against Carlsen.
While this episode has dominated the headlines, the threat of cheating is not entirely new to the game. In the 2010 FIDE (International Chess Federation) Olympiad Tournament, French Grandmaster Sebastian Feller was found guilty of using a computer program to suggest moves, a decision that cost him his gold medal.3 During both the Zadar Open in 2012 and a tournament in Kyustendil in 2013, Borislav Ivanov was accused of cheating, as was Igors Rausis in the 2019 Strasburg Open, and Tigran Petrosian in the 2020 Pro Chess League.4
The potential to cheat has been driven primarily by the development of chess ‘engines’: computer algorithms that are able to calculate the moves needed to defeat the greatest human players.5 These engines can be downloaded onto players’ phones and used both in over-the-board (OTB) tournaments and online.
This threat has been taken seriously by various chess organisations, with the FIDE and the Association of Chess Professionals (ACP) establishing the joint ‘FIDE/ACP Anti-Cheating Committee’ in 2013.6 In serious OTB tournaments, physical security checks are undertaken to determine whether players have earpieces or other electronic equipment on their person that could be used by an accomplice with an engine to transfer move suggestions. Alongside this are algorithmic detection measures, which are the subject of this article.
While online chess platforms such as Chess.com and Lichess likely have their own anti-cheating detection systems, the details of these have not been publicised. The focus of this article is therefore the detection method used by FIDE, which was prepared by Kenneth Regan, Professor of Computer Science at the University of Buffalo, USA (the ‘Regan system’).
Methods of cheating detection
The Regan system works by estimating an ‘Elo’ for a player based on the moves that they have played in a game or tournament, or across a period of time. A player’s Elo is a numerical score that is used by chess websites and FIDE to keep track of the player’s strength. The Elo estimated by the Regan system, which Regan refers to as an Intrinsic Performance Rating (IPR), is then compared against that same player’s ‘actual’ Elo, which they will have received from a chess body (such as FIDE if they play in FIDE-accredited tournaments) based on their previous performances in chess games.
If the IPR is substantially higher than the player’s actual Elo then it may be that they are cheating. This is because, since at least the 1990s, chess engines have been able to beat the best human chess players, and are now considerably superior to them. Therefore, if a player has used a chess engine (which is easy to do online, but requires a higher level of deception when playing OTB), their moves may look too good to have been played by a human.
In what follows, we outline the four steps of the Regan system, as shown in Figure 1 below.7
Figure 1 Steps of the Regan system

Step 1: calculating the drop-off from the best move
The algorithm starts by considering all the positions that a player assessed across the games in which their performance is being evaluated. A chess engine analyses each position, and calculates the quality of moves that the player could make.8
The best move is the move that gives a player the largest possible advantage (or smallest disadvantage), measured in terms of the difference in the number of ‘effective pawns’9 between the two players. The engine will also evaluate each position for other moves (again measured in terms of the difference in effective pawns), and it is therefore possible to calculate the difference between the evaluation that an engine gives for the best move, and the evaluation for other, inferior moves. The better the move that a player selects, the closer it will be scored to the best move, and therefore the lower the ‘drop-off’ will be from the best move.
Step 2: calculating the partial credit, sensitivity and consistency
Other considerations then come into play. A player with a lower value for the ‘sensitivity’ parameter in the algorithm is better able to discriminate between moderately inferior move choices. The ‘consistency’ parameter reflects a player’s ability to avoid making poor moves.10 ‘Partial credit’ (y) is defined as a function of sensitivity (s), consistency (c) and the drop-off (d) as follows:
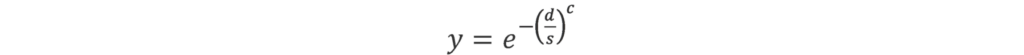
The sum of all the partial credits must add up to the ‘full credit’ for a particular move. This means that, when there is one move that is clearly better than all others, it will have high partial credit because there is very little ‘credit’ associated with playing other moves.11 However, if there are a lot of moves of a similar quality, the partial credit will be split more evenly across the moves.
The relationship between partial credit and the drop-off can be seen in Figure 2 below.
Figure 2 Distribution of partial credit
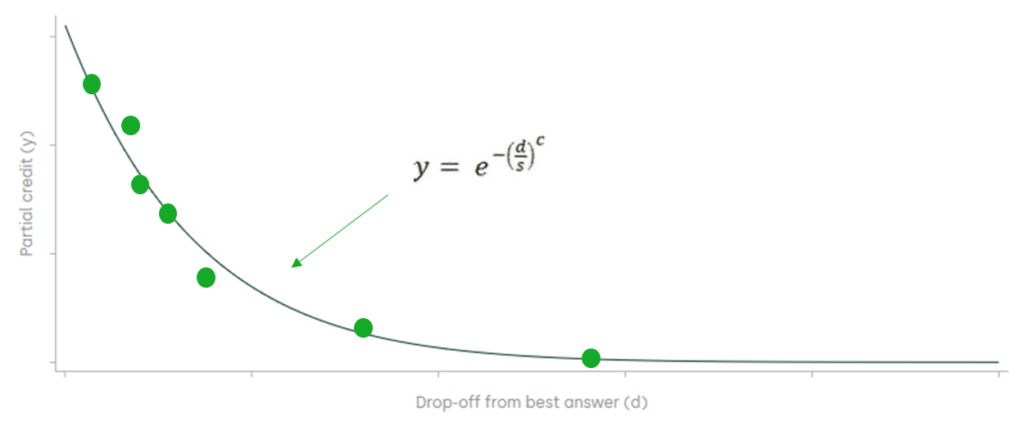
Source: Oxera elaboration of Figure 3 in Goldowsky, H. (2014), ‘How to Catch A Chess Cheater: Ken Regan Finds Moves Out Of Mind’, Chess Life, June.
The precise shape of the partial credit curve is also affected by the values of the sensitivity and consistency parameters. Figure 3 below shows that a curve with higher consistency will hug the y-axis, representing the fact that players with a higher consistency will play more moves that have high partial credit. Intuitively, this means that better players will tend to avoid moves with a high drop-off from the best move (i.e. they will avoid bad moves), irrespective of the number of moves they have to choose between in a particular position.
Figure 3 Relationship between partial credit (y) and drop-off (d) for different values of consistency (c)
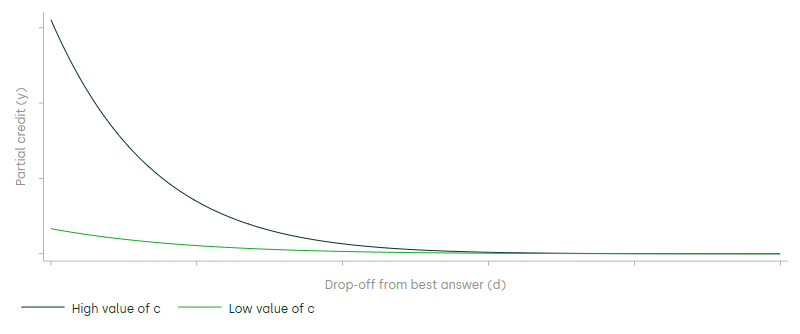
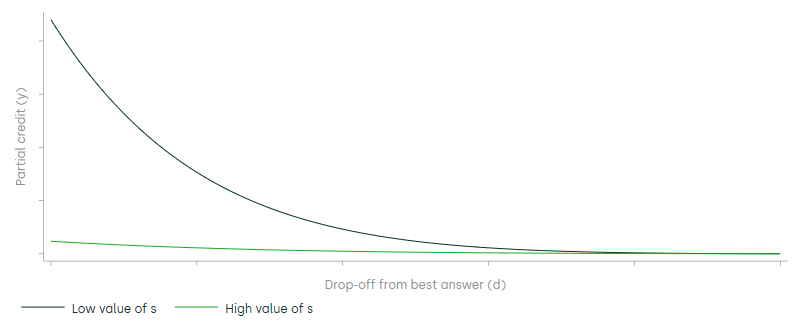
Figure 4 shows how a decrease in sensitivity lowers the curve for any given value of the drop-off. This represents the fact that better players will be able to discriminate between small differences in move quality, because they play moves that account for a higher proportion of the total credit associated with a position.
Figure 4 Relationship between partial credit (y) and drop-off (d) for different values of sensitivity (s)
Step 3: converting the sensitivities and consistencies into an IPR
As shown above, better players (with higher consistency and lower sensitivity) will have higher curves that hug the y-axis more tightly, reflecting the higher expectation they will find and play the better moves. Step 3 of the Regan system generates a player’s IPR based on the player’s curve.12
Table 1 shows, for a sample of s and c values, the IPRs that different combinations of sensitivity and consistency correspond to. For example, a player with a consistency of around 0.515, and a sensitivity of around 0.082, will have an IPR of 2,700. As the IPR is an estimated Elo, and an Elo of 2,700 would be achieved by a strong Grandmaster (a ‘Super GM’), this would indicate that the player has performed at Super GM level.
Table 1 Examples of conversions of sensitivities and consistencies into IPR

Step 4: testing whether a player’s performance is materially different to what is implied by their Elo
As mentioned above, each chess player will have an ‘actual’ Elo that corresponds to how well they have played in previous games in their career. A player’s Elo will increase when they win games (and the stronger the opponent, the greater the player’s increase), and vice versa. Drawn games will typically result in little movement in a player’s Elo, unless the player who they drew against was substantially better than they were (in which case their Elo will increase) or substantially worse (in which case their Elo will fall).
A player’s IPR can then be compared against their ‘real-life’ Elo. However, a simple comparison of the IPR and the Elo would ignore the statistical uncertainty around the IPR estimate, and Regan therefore applies ‘z-scores’ to his comparisons.13 A z-score is a well-known statistical technique for identifying outliers. The greater the z-score, the greater the difference in the performance of the player relative to a typical player with the same Elo rating. This could indicate that the player is more likely to have cheated.
In chess, the threshold that is applied to the z-score (i.e. to determine whether a player is likely to have cheated) is 4.5. As a z-score of 4.5 means that the probability that a player played the moves they did without assistance is 1 in 300,000—this means that only extreme performances place players under suspicion of cheating. It is notable that, when Professor Regan reviewed Niemann’s performance against Carlsen, his system did not conclude that Niemann was likely to have cheated.14
Potential issues with the Regan system
The Regan system is not without its problems.
When picking a threshold for a statistic such as a z-score, one must remember that it introduces a trade-off between the probabilities of making type I and type II errors.15 Type I errors (false positives) occur when a player is falsely identified as having cheated, and type II errors (false negatives) occur when a player is falsely identified as not having cheated. Setting a higher threshold for a z-score will result in more false negatives, but also fewer false positives.
There is no perfect level at which the threshold should be set. Setting a high threshold increases the risk that real cheaters will be missed. Setting a low threshold increases the risk that an innocent player with a string of good moves will be branded a cheat. The balance of these risks, as in other contexts in which statistical tests are applied, is a matter of judgement. The threshold of one in 300,000 that is applied by Regan corresponds to a high bar for someone to be under suspicion of cheating. This is because it requires them to perform at a level that would be expected to arise by chance only once every 300,000 games for a player of their skill level.
The correct threshold will also depend on the strategies that chess cheaters use. If they are ‘smart’, they may overall perform only slightly better than their Elo suggests, while if they are not, they may perform considerably better. Smart cheating might involve, for example, using only a second- or third-best move,16 or consulting the engine only for selected moves in the game. In games that are played by top players, such as the one between Carlsen and Niemann, there may be only one or two key instances where a player struggles to evaluate potential moves, and therefore where the support of a chess engine could be helpful.
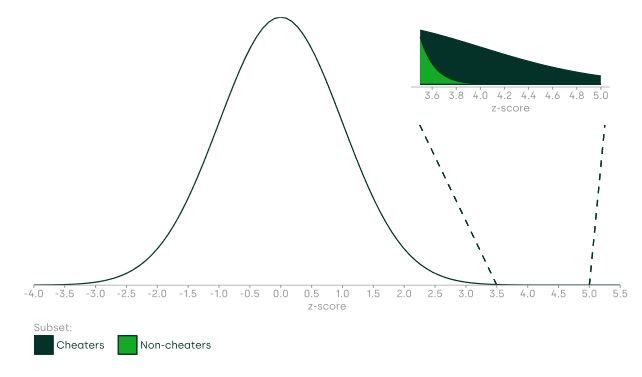
If most cheaters are not smart, a larger proportion of individuals with z-scores of around 4.5 are likely to be cheaters, and fewer of the individuals with lower z-scores are likely to be cheaters. This is shown in Figure 5 below. A very high z-score reflects a performance that is considerably better than the actual Elo of a given player, whereas a very low z-score reflects a performance that is considerably below the Elo of a given player. Average z-scores represent players who perform roughly in line with expectations, which is why the curve is tallest at this point (i.e. most of the time, people play at the level you would expect of them).
In a situation with a high proportion of cheaters who are not smart, using a high threshold such as 4.5 could be appropriate, as the majority of individuals with z-scores above 4.5 would be cheaters, while those with scores below it are less likely to be.
Figure 5 Distribution of players’ games and associated z-scores (I)
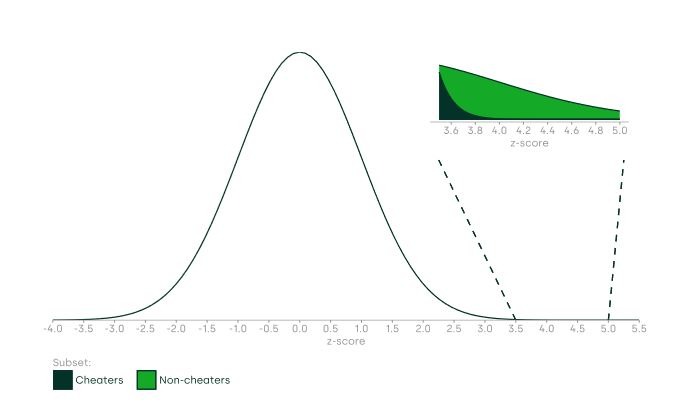
However, if most cheaters are smart, they may perform only slightly better than expected based on their Elo, which will result in most of the players who receive z-scores of around 4.5 being non-cheaters. This is illustrated in Figure 6 below, which applies the same underlying assumptions as in Figure 5, but this time assumes that a greater proportion of cheaters apply smart cheating strategies to avoid detection.
Figure 6 Distribution of players’ games and associated z-scores (II)
Other factors could also result in non-cheaters playing unusually well and therefore receiving high z-scores (occasionally even above the 4.5 threshold). A quickly developing chess prodigy will consistently perform better than their Elo suggests. A player using an obscure or innovative line might surprise their opponent—and a player could just be having an unusually good day. Furthermore, in the immediate post-COVID-19 period, many players (especially young players such as Niemann—young players’ development is typically quicker than that of older players) may be playing at levels above their Elos, as they could have used the pandemic period to train but would not have been able to play competitive OTB games.
Indeed, there is good evidence that non-cheaters can receive high z-scores for their performance. Barnes and Hernandez-Castro (2015) analysed 120,000 games that took place before 2005, and found that the application of the Regan system would result in at least 92 of the players being identified as suspicious.17 However, all these games happened when cheating with a chess engine would have been near-impossible, as publicly available engines were not strong enough, and they required computing power at a level that was generally unavailable outside research institutions and technology companies at the time.
Alternative ways of identifying cheating
Lichess and Chess.com are likely to have their own methods for detecting cheating, but these will be proprietary and have therefore not been reviewed in this article. However, research into cheating detection suggests that material improvements over the Regan system will be difficult to realise in practice, as explained below.
One avenue of research is to combine position evaluation (as in the Regan system) and pattern recognition using various machine-learning models. Patria et al. (2021) applied deep-learning techniques to a dataset of 5,000 games of cheater and non-cheater players that took place on Lichess.18 The idea behind applying pattern recognition to detect cheating is that it is possible that there are some common patterns among cheaters that cannot be picked up by either the human eye or a pure engine evaluation. These models were able to detect cheating in only 52–57% of games that were outside of the data they were trained on, which is barely better than a random guess.
Where next for cheating detection?
The approach taken to detect cheating in chess suffers from clear limitations. Specifically, by identifying only those individuals who play a 1 in 300,000 game, there is a risk that less regular cheaters or ‘smart’ cheaters will not be caught by the Regan system. In the context of the Carlsen vs Niemann saga, Regan’s algorithm does not appear to be well placed to identify whether top-level players, who need minimal engine assistance, do occasionally consult a chess engine.
Despite this, there does appear to be a need for additional improvements. The machine-learning algorithm discussed above relied on a small number of datapoints. Furthermore, in order to classify whether the move was undertaken with the assistance of an engine, it had to assume that, if the player had been banned for cheating, they had cheated on that specific move. A larger dataset and a more accurate encoding of whether moves were played by cheaters or non-cheaters would probably result in improved machine-learning models—but gathering this data is easier said than done.
Researchers could also consider adding new variables to their analyses. For example, the Regan system does not currently appear to explicitly consider the difference in how a human player would evaluate a position, and how an engine would evaluate a position as a potential input variable. The intuition behind this is that regularly selecting best moves is more suspicious if those moves can be identified only with deep-engine analysis. Such a variable could perhaps be constructed by considering the change in a particular move’s evaluation when a chess engine moves from a shallower to a deeper depth.19
Alternatively, chess websites could gather data on how humans perceive different positions by uploading positions that players accused of cheating faced as ‘puzzles’, and seeing how often those puzzles are solved by users. If few players, even those with a high Elo, correctly solved the puzzle, this could indicate that the move was likely to be suggested by an engine.
In future, datasets could also be expanded to cover physiological characteristics such as pulse, sweat or facial expressions.
Cheating in chess echoes, and potentially foreshadows, technologically induced problems in other areas of society. Chess engines offer clear benefits to players. A player studying chess with an engine as an assistant can benefit from a deeper understanding of chess positions, and a clearer view of their mistakes. They are given the potential to improve faster and further than would ever have been possible in previous decades.
However, the technology to enhance performance is racing ahead of the technology to detect enhancement. In an environment characterised by close competition and thin margins, it is easy to appreciate how the line between ‘beneficial teaching aid’ and ‘nefarious cheating aid’ can be so frequently crossed.
As AI technology continues to move forward, analogous problems are arising in other competitive sectors. Exams and coursework in schools and universities, and academic publishing, are increasingly having to engage with the impact of language-based AIs such as ChatGPT. Other sectors may face similar questions as machines take the edge over humans in terms of speed or acuity. Activities from poker to job applications and poetry slams may all find themselves grappling with the same possibility of ‘AI doping’ that has shaken the world of chess.
Regrettably, for now, the chess experience of algorithmic detection offers no simple answers. Instead, tournament organisers are moving to face-to-face tournaments and physical searches of players, and accepting the costs that these involve. Not every high-tech problem has a high-tech solution.
1 Carlsen, M. (2022), ‘My statement regarding the last few weeks’, tweet, 8.35pm 26 September.
2 United States District Court Eastern District of Missouri: Eastern Division (2022), Hans Moke Niemann v. Sven Magnus Øen Carlsen A/K/A Magnus Carlsen, Play Magnus AS D/B/A Play Magnus Group, Chess.com, LLC, Daniel Rensch A/K/A “Danny” Rensch, and Hikaru Nakamura, 20 October.
3 See Doggers, P. (2015), ‘Sebastian Feller Can Play Chess Again’, Chess.com, 8 May.
4 See Mistreaver (2019), ‘Cheating in chess: A history’, Chessentials, 6 August; Evergreen_Warrior (2020), ‘Latest News – Armenia Eagles Disqualified, Saint Louis Arch Bishops Wins PCL 2020’, Forums post, 1 October.
5 A chess engine analyses chess positions and returns what it calculates to be the best move options. In the chess world, several chess engines are well-established legitimate tools. See Chess.com, ‘Chess Engine’.
6 FIDE, ‘Anti-Cheating Guidelines’, p. 2.
7 See Goldowsky, H. (2014), ‘How To Catch A Chess Cheater: Ken Regan Finds Moves Out Of Mind’, Chess Life, June; Holowczak, A. (2020), ‘The King of Lockdown’, Chess, 85:8, p. 22; Zaksaitė, S. (2020), ‘Cheating in chess: a call for an integrated disciplinary regulation’, Kriminologijos studijos, 8, pp. 57–83.
8 The evaluation of a chess position depends on three factors: (i) the list of candidate moves; (ii) the maximum depth selected; and (iii) the heuristic nature of the engine’s evaluation function. See Di Fatta, G., Haworth, G.M. and Regan, K.W. (2009), ‘Skill Rating by Bayesian Inference’, March; Institute of Electrical and Electronics Engineers (2009), ‘Symposium on Computational Intelligence and Data Mining’, pp. 89–94.
9 An advantage of 0.76 pawns, for example, means that a player has 0.76 more pawns of their colour relative to their opponent’s colour.
10 Regan, K.W., Macieja, B. and Haworth, G.McC. (2012), ‘Understanding Distributions of Chess Performances’, Advances in Computer Games 2011, conference paper, pp. 230–43.
11 Goldowsky, H. (2014), ‘How To Catch A Chess Cheater: Ken Regan Finds Moves Out Of Mind’, Chess Life, June.
12 Goldowsky, H. (2014), ‘How To Catch A Chess Cheater: Ken Regan Finds Moves Out Of Mind’, Chess Life, June.
13 The z-score measures how many standard deviations below or above the player’s typical Elo rating performance a player’s test performance is. See Glen, S., ‘Z-Score: Definition, Formula and Calculation’, StatisticsHowTo.com: Elementary Statistics for the rest of us!.
14 Silver, A. (2022), ‘Is Hans Niemann cheating? – World renowned expert Ken Regan analyzes’, ChessBase, 20 September.
15 See Bhandari, P. (2022), ‘Type I & Type II Errors | Differences, Examples, Visualizations’, Scribbr, 11 November.
16 See Barnes, D. and Hernandez-Castro, J. (2015), ‘On the Limits of Engine Analysis for Cheating Detection in Chess’, Computers & Security, 48, pp. 58–73.
17 See Barnes, D. and Hernandez-Castro, J. (2015), ‘On the Limits of Engine Analysis for Cheating Detection in Chess’, Computers & Security, 48, pp. 58–73.
18 Patria, R., Favian, S., Caturdewa, A. and Suhartono, D. (2021), ‘Cheat Detection on Online Chess Games using Convolutional and Dense Neural Network’, 4th International Seminar on Research of Information Technology and Intelligent Systems (ISRITI). The authors used two types of neural network model—dense and convolutional.
19 In chess, engine depth refers to the number of half-moves (a move taken by one player—a full move is when both players take a move) into the future that an engine looks at when evaluating a position.
Related

Measuring and inferring anticompetitive effects from an exchange of information
In four rulings1 dated 3 November 2025, the Spanish National Court overturned the Decision of the Comisión Nacional de los Mercados y la Competencia (CNMC) in case S/DC/67/17 Tabacos2 (‘the Decision’). These four rulings are significant because they close one of the first cases that the… Read More

Decoding the Digital Networks Act: the future of the EU electronic communications and digital infrastructure regulatory framework
On 21 January 2026 the European Commission published the long-awaited draft of its Digital Networks Act (DNA)—the proposed new regulation that seeks to ‘modernise, simplify and harmonise EU rules on connectivity networks’.1 As the draft is now being reviewed by the European Parliament and the Council, representing the… Read More

