A beautiful mind: the Nash legacy
John Nash, who died last month, changed the world of academia forever. His work in theoretical mathematics, bargaining theory and development of the Nash equilibrium has had a huge impact on a wide range of fields, including political science, international relations, philosophy and economics. Practitioners such as Oxera owe Nash a huge debt. Many of the theories about how firms interact, and how markets work, come directly from his work on game theory
Many will know John Nash as the mathematician depicted in the Oscar-winning film, A Beautiful Mind. While that film is a compelling insight into the struggles that came to define much of his life, it is important to remember that the reason the film was produced in the first place was due to Nash’s brilliant and influential insights during the 1950s. The fact that he made his mark through just five academic papers during a ten-year timespan attests to what a remarkable person he was.1
Nash’s contributions to industrial organisation theory, and hence competition and regulatory economics, can be classified into two types: he helped to develop the framework that we use to think about how firms interact—that of ‘non-cooperative games’; and he came up with a way of working out what the outcome of that interaction will be—his famous namesake ‘equilibrium’.
A game describes any situation in which two or more ‘players’ (e.g. people or firms) can perform actions (strategies) that affect not only their own ‘payoffs’ (e.g. profit), but also the payoffs of other players with whom they interact. While Nash did not invent the theory of games, his seminal contribution was in the development of non-cooperative game theory.2
‘Cooperative’ game theory, which had preceded this, assumed that players could enter into formal coalitions and bargain over a given portion of the available pie—a ‘zero-sum’ game in which one player’s loss exactly matched another player’s gain.3 Nash himself developed cooperative game theory in the form of what has become known as Nash bargaining—now often referred to in the context of setting FRAND (fair, reasonable and non-discriminatory) terms in patent licensing.4 However, he recognised that this did not consider the full range of situations—what if players were unable to formally cooperate or communicate with one another? What if the overall size of the available pie depended on the various players’ actions?5
The mathematical foundations of non-cooperative game theory laid by Nash helped economists to gain a better understanding of firm behaviour, beyond the somewhat stringent assumptions of monopoly (in which there are no other firms to worry about, and thus no interactions) and perfect competition (in which there are many small firms, such that no one firm can influence the strategy of another). It led to a much richer understanding of oligopoly, in which a few firms interact and receive payoffs that are determined by each other’s actions. In this setting, each firm needs to set prices (or quantities) in a way that maximises its profits, given what its rivals are doing. Nash’s equilibrium is then a way of working out what each firm’s strategy will be.6
This resulting equilibrium is not necessarily ‘optimal’ for the players, in terms of leading to the best outcome. Rather, in a two-firm situation, a Nash equilibrium is where Firm A is setting prices (or quantities) to make the most profit it can, taking Firm B’s strategy as given, while Firm B is also doing the best that it can, taking Firm A’s strategy as given. That is, it is a stable outcome in which neither firm, through unilaterally changing its own strategy, can increase its profits. A Nash equilibrium may not always exist, but it often does,7 and if more than one Nash equilibrium exists in a game, which one will be reached is unclear.8 However, if both players have a ‘strictly dominant’ strategy—i.e. one that makes them better off regardless of the other player’s strategy—the game has one unique Nash equilibrium outcome.
The prisoners’ dilemma
It may be easier to understand the concept of a Nash equilibrium through a familiar example in economics—the ‘prisoners’ dilemma’.9 Here, two prisoners are locked in different interview rooms at a police station, and are not allowed to communicate. They have two options: refuse to say anything, or accuse the other prisoner of committing the crime. If neither says anything, due to a lack of further compelling evidence, the police can convict them only on lesser charges, and they each go to prison for one year. If one accuses the other of the crime, and the accused prisoner says nothing, the latter will go to prison for five years (and, as a reward for this helpful information, the accuser will go free). Finally, if each accuses the other, by implicating one another, both will go to prison for two years.
The prisoners get ‘one shot’ at this game. Assuming that they want to spend as little time in prison as possible, the optimal outcome—at least from the prisoners’ perspective—would be for both to stay silent. After all, one year in prison is better than two, and one year is certainly better than five years. But is this outcome a Nash equilibrium? To answer this question, let’s assume that the ‘disutility’ (i.e. negative impact) experienced by the prisoners corresponds precisely to the number of years they would face in prison. So the payoffs for Prisoner A and Prisoner B, respectively, from both remaining silent are (-1, -1); that is, one year each in prison. If, however, each accuses the other, they will each receive a two-year sentence, or payoffs of (-2, -2). Finally, if A accuses B while B remains silent, the payoffs are (0, -5), and if B accuses A while A remains silent, the payoffs are (-5, 0). Figure 1 presents a matrix summarising these strategy/payoff combinations.10
Figure 1 The prisoners’ dilemma game
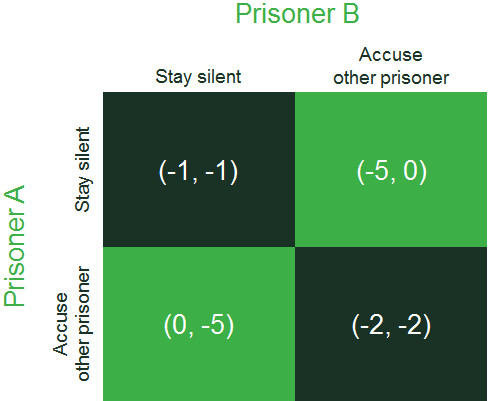
Source: Oxera.
Given these payoffs, we can now find the Nash equilibrium. Starting with Prisoner A, who gets to choose between the top and bottom rows in Figure 1, if B chooses to stay silent, A would prefer to accuse (0 is preferred to -1). If, however, B accuses, A would again prefer to accuse (-2 is preferred to -5). Thus, whatever B does in this game, A’s best reply is to play the bottom row strategy—to accuse B. This is therefore a strictly dominant strategy. Prisoner B, who simultaneously gets to choose between the left-hand and right-hand columns, faces the same situation: whatever A does, B’s best reply is to accuse.11
By the above process of elimination, therefore, the Nash equilibrium is the outcome where the prisoners accuse each other of committing the crime. Neither prisoner, having committed to the strategy of accusing the other, would want to unilaterally change their decision. While both prisoners would prefer the optimal outcome (-1, -1), which would be obtained through cooperation, they cannot commit to this, and so they receive (-2, -2).
The Nash equilibrium in economics
The prisoners’ dilemma is a simple game that may seem somewhat abstract relative to how firms interact in markets. However, it is a useful metaphor for explaining certain forms of oligopoly behaviour, in terms of whether firms choose to simultaneously set high or low prices. Take, for example, a standard Bertrand model (a competition model in which firms compete on price) between two firms selling identical goods (a duopoly), where the firms can increase (or decrease) their output as they please. In an ideal world, the firms would wish to set high prices, as this means high profits. Such prices might be obtained if they sat in a smoke-filled room and colluded. However, if the firms are not able to cooperate, is this outcome possible?
In this game, since the firms sell identical products and neither faces capacity constraints, by lowering prices by a very small amount, one firm is able to capture the whole of the market at the expense of the other.12 Both parties realise that this is a dominant strategy, and hence, while both would be better off charging high prices, they actually compete prices down to a low level (such that prices equal marginal cost).
This is a somewhat paradoxical result—that a model of oligopoly with just two firms, and with strategic interaction, generates the outcome that might be expected under perfect competition (i.e. between many small firms). However, this is not a flaw in the Nash equilibrium concept. Rather, it is a consequence of the assumptions made about the game being played, the intensity of interaction, and the associated payoffs. For one-shot games, models of Cournot competition (in which firms set quantities rather than prices),13 and product differentiation (in which products are not perfect substitutes), produce Nash equilibria in which the resulting prices are above marginal cost.
Many models of oligopoly developed by industrial economists since the 1950s have sought to resolve the ‘Bertrand paradox’, or how prices above marginal cost (a theoretical measure of market power) can be sustained in Nash equilibrium. They have been assisted by a number of refinements to the Nash equilibrium concept. Notably, the approach described above considers one-shot games in which players make their decisions simultaneously. However, in games in which players move sequentially—‘dynamic games’—certain Nash equilibria may not be credible.
Take a two-player dynamic game in which player 1 is considering whether to open a store next to player 2’s existing store. Player 2 threatens to engage in a price war should this happen. If player 1 believes this, it may choose to abandon its plans. This may be one Nash equilibrium of the game. However, what this ignores is that, once player 1 has made its move, this is a fait accompli, and player 2 will simply need to do its best given the situation. Player 2 may threaten to punish player 1 through aggressive action but, if this strategy is not optimal for player 2 once player 1 has moved, the threat will not be credible. Nash equilibria that rely on non-credible threats can be eliminated through ‘backward induction’—start from what is optimal for player 2, given the various strategies that player 1 might play, and work backwards to figure out what player 1 would do in the first instance. The outcome is a sub-game perfect (Nash) equilibrium (SPNE).14 This concept has, for example, been applied to models in which an incumbent firm commits to deterring entry by other firms by engaging in below-cost (or predatory) pricing. This commitment may not be credible if, once the entrant has entered, it makes more sense for the incumbent to acquiesce (i.e. price above cost). However, predatory pricing becomes more credible as a threat if the game is repeated an infinite or indefinite number of times, or there is some uncertainty in the mind of the entrant as to the incumbent’s costs of predation and payoffs (including whether the incumbent has an innate predisposition to predate).15
The concept of SPNE moreover applies to ‘repeated games’ in which a simultaneous game is played a number of times (for example, the prisoners’ dilemma). In a Bertrand game between two firms that is repeated, does the repeated setting lead to a situation in which the firms set high prices? In this case, the place to start is the result of the final game which, if the players are rational, will mean that both set low prices (the Nash equilibrium outcome of the one-shot game). Using backward induction, we then can determine that any attempt to set high prices essentially unravels, and that every preceding game will result in low prices. However (once again), if the game is infinitely repeated, or there is a chance that it might end at any point, the situation changes, as ‘tacit collusion’ may be sustained as an SPNE. As long as both firms care enough about the future and have a low enough discount rate, both may choose to set high prices, with the credible threat that, should the other firm set low prices, they will follow suit as punishment.16 In general, the fewer firms that are present, the easier it is to monitor defection; and the more the parties care about the future, the more likely it is that tacit collusion can be sustained.
Concluding thoughts
The non-cooperative game theory framework pioneered by John Nash, and the concept of the Nash equilibrium, have had a huge impact on industrial economics and, by extension, competition policy. There have been a number of refinements to his framework since the 1950s, but these are perhaps best regarded as exactly that—refinements, rather than direct challenges. Nash’s framework set the groundwork for economists to examine key issues such as whether market power is present, whether predation is feasible, and whether mergers might give rise to concern about tacit collusion. His mathematical contributions have thus left a lasting legacy in both economic theory and competition policy around the world.
[1] A list of these works is provided in The Nobel Foundation (1994), ‘The work of John Nash in game theory’, Prize Seminar, 8 December.
[2] Nash, J.F. (1951), ‘Non-cooperative games’, Annals of Mathematics, 54, pp. 286–95.
[3] Von Neumann, J. and Morgenstern, O. (1944), Theory of Games and Economic Behavior, Princeton University Press. These authors also proposed a ‘minimax’ solution for a restricted class of non-cooperative game—two-person zero-sum games.
[4] Nash, J.F. (1950), ‘The bargaining problem’, Econometrica, 18, pp. 155–62; and Nash, J.F. (1953), ‘Two-person cooperative games’, Econometrica, 21, pp. 128–40.
[5] Nash also considered what might happen if there were any number of players (rather than just two).
[6] Augustin Cournot had previously set out a quantity-setting duopoly non-cooperative one-shot game. Nash generalised the approach to a wider number of settings. See Cournot, A. (1838), Researches into the Mathematical Principles of the Theory of Wealth, Macmillan.
[7] If the players are constrained to ‘pure’ strategies only (actions that they must choose with certainty), a Nash equilibrium is not guaranteed. Examples in which no pure strategy Nash equilibria exist are two-player ‘matching pennies’ and ‘scissors-paper-stone’ (intransitive games). Nash proved, however, that an equilibrium always exists in a finite game if players are allowed to play ‘mixed’ strategies, in which different pure strategies are played with assigned probabilities.
[8] Examples of games with more than one Nash equilibrium include two-player ‘driving on the left or right’ and ‘Bach or Stravinsky’. As will be discussed, some games have more than one Nash equilibrium but, due to the order of the game, some equilibria will be more ‘credible’ than others.
[9] This was first proposed in Tucker, A.W. (1950), ‘A two-person dilemma’, Mimeograph, Stanford University, Stanford.
[10] This matrix is called the ‘normal form’ of the game.
[11] In this simultaneous one-shot game with complete information, it is therefore possible to eliminate the strictly dominated strategy of ‘stay silent’.
[12] In the Bertrand game there is a discontinuity in payoffs, which drives the result: reducing the price by a very small amount leads to the undercutting firm gaining 100% market share.
[13] In contrast to the Bertrand model, the Cournot model does not have discontinuity in the payoff function—i.e. if one firm increases its quantity by a small amount, this does not lead to a large change in market share.
[14] SPNE was formalised in Selten, R. (1965), ‘Spieltheoretische Behandlung eines Oligopolmodells mit Nachfrageträgheit’, Zeitschrift für die Gesamte Staatswissenschaft, 121, pp. 301–24 and 667–89. A Nash equilibrium is sub-game perfect if the players’ strategies constitute a Nash equilibrium in every sub-game.
[15] For a discussion of the ‘chain store paradox’, which examines whether predation is a likely strategy, see Selten, R. (1978), ‘The Chain Store Paradox’, Theory and Decision, 9, pp. 127–59; and Kreps, D. and Wilson, R. (1982), ‘Reputation and Imperfect Information,’ Journal of Economic Theory, 27, pp. 253–79.
[16] However, the focal price obtained is not clear (there is a range of plausible equilibrium prices).
Download
Related

Ofgem’s RIIO-3 Sector Specific Methodology Decision
On 18 July 2024, Ofgem published its Sector Specific Methodology Decision (SSMD) for the forthcoming RIIO-3 price control period for electricity transmission (ET), gas transmission (GT) and gas distribution (GD) networks.1 This follows Ofgem’s consultation on the matter in December 2023.2 RIIO-3 will last for… Read More

The future funding of the England & Wales water sector: Ofwat’s draft determinations
On Thursday 11 July, Ofwat (the England and Wales water regulator) published its much anticipated Draft Determinations (DDs). As part of the PR24 price review, this sets out its provisional assessment of allowed revenues and performance targets for AMP8 (2025–30)—and will be of great interest to water companies, investors,… Read More

