Which WACC when? A cost of capital puzzle (revisited)
Real or nominal? Pre-tax or post-tax? (Or even vanilla?) The number of ‘flavours’ for calculating the weighted average cost of capital is sometimes bewildering. It is often assumed that they all reach more or less the same conclusion, but is this always the case? Contrary to common belief among practitioners, different styles of calculation have a material impact on the value of cash flow to investors.
This article was originally published in September 2005. All 2015 commentary is from Oxera.
How should a regulator estimate the weighted average cost of capital (WACC) of the companies it regulates? Twenty years of regulatory precedent have not managed to simplify the issue, and it remains central to any price-setting process.
This article discusses the relationship between the cost of capital, inflation and tax in the context of utility regulation. However, the concepts are applicable whenever conversions between pre- and post-tax, or real and nominal costs of capital are required. For example, profitability analysis is frequently undertaken based on pre-tax cash flows, and benchmarked against a pre-tax cost of capital. As the article shows, it is easy to miscalculate the pre-tax cost of capital and thereby introduce bias into the analysis.
Recently, attention has focused increasingly on precisely which version of the WACC should be used. Numerous possibilities exist, differing, in particular, in the way they approach two key issues. The first is the approach taken to compensating investors for the effects of inflation; the second is the way in which a company’s tax liability is remunerated.
This article investigates why regulators are looking again at this issue. In the recent distribution price control review (DPCR4), Ofgem changed its approach to funding the tax liabilities of the distribution network operators; meanwhile, Network Rail’s interim review of track access charges has suggested a different approach to dealing with the effect of inflation.1 It is recognised that the approach to both issues can affect, for example, the incentives on the capital structure of firms and the extent to which a price control package is believed to be ‘financeable’.
There is, however, a bigger issue. It is often assumed that even when approaches to the WACC differ, the long-term effect is the same. That is, the revenues received by the company, and the cash flows they provide to investors, are the same under any of the approaches.
As discussed in this article, this is not always the case.
- Regulators account for the effects of tax and inflation in a variety of ways within their price-setting frameworks.
- These differences can have an impact on factors such as financeability and the incentives to adopt particular capital structures.
- It is assumed that the long-term result is the same regardless of which approach is taken. This is not always correct.
First, inflation
Inflation is central to regulation. It is a given, in the UK and abroad, that investors’ returns should allow for inflation, and that what matters are the real returns received by investors.
Real returns
The meaning of real returns depends on the inflation index that nominal returns are benchmarked against, and is ambiguous unless this index is specified. It is usual practice to use an index of consumer prices, and in many countries there is an obvious index to choose. For example, there is a harmonised methodology for calculating consumer price indices across EU countries. In the UK, there are two broad groups of consumer price indices—the Retail Prices Index (RPI) and the Consumer Prices Index (CPI)—along with variants of these such as RPIJ and CPIH. These were reviewed in a February 2015 Agenda article.1
1 Oxera (2015), ‘Is the end nigh for RPI?’, Agenda, February.
There are two ways in which this can be achieved. The first is typical of the majority of UK regulatory precedent. Inflation is compensated for through annual indexation and applied to the assets on which a real return is allowed. The second approach is to wrap expectations of inflation into the nominal WACC calculation. Here, the regulatory asset base (RAB) is not adjusted to allow for inflation; the necessary compensation is provided by the WACC calculation itself.
If it is assumed for the moment that both approaches have the same long-term result, what factors influence the appropriateness of each approach?
As mentioned above, the typical UK approach is for the RAB to be indexed by inflation and a real WACC to be used. This approach has one important advantage: in real terms, the regulatory depreciation allowance is constant in each year that the asset remains within the asset base (assuming straight-line depreciation). As a result, today’s customers and tomorrow’s customers pay an equal amount for the asset. This reflects the fact that both sets of customers derive benefit from the use of the asset.
However, this approach also has a disadvantage. It can mean that the way the company remunerates its investors differs from the way consumers remunerate the company. Figure 1 shows why this is important. It assumes that a debt of £1,000 attracts a nominal interest rate of 6.6%, and that it is necessary to repay £100 of the principal in every year. But what if that debt was used to finance a £1,000 investment, depreciated over ten years, with a return of 4.0% allowed and the RAB indexed by inflation at 2.5%?
The results are very different. When debt is raised, the interest paid is normally expressed on a nominal basis with no indexation of the principal. This results in interest costs having a relatively ‘front-end loaded’ profile, while the remuneration of the costs provided for in the regulatory settlement is ‘back-end loaded’.
Figure 1 Interest costs and associated remuneration
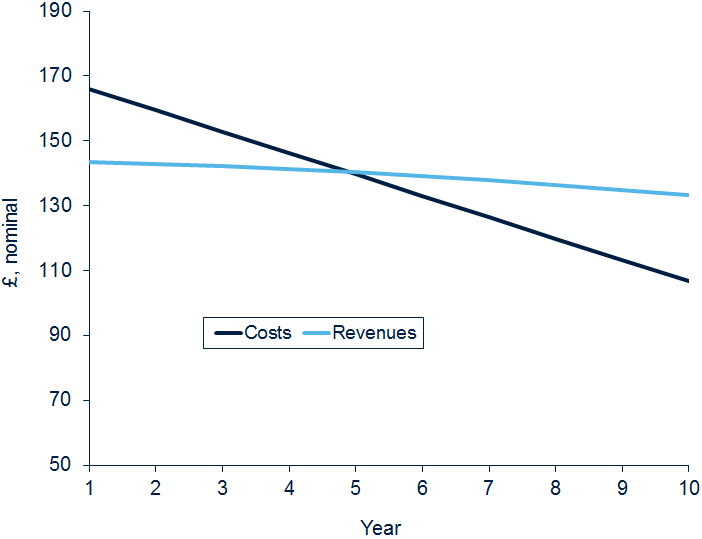
This difference can have significant policy implications. In a regulatory environment in which, in many sectors (particularly the water sector), there is already considerable concern regarding the financeability of the regulatory package,2 a regulatory policy that exacerbates the difference between costs being incurred and revenues for their remuneration provided—i.e. using indexing and real WACC—strikes some as curious. This was certainly the view of Network Rail during the 2003 interim review of track access charges, and it is also a point that has been raised (in a personal capacity) by Lord Currie, Chairman of Ofcom.3
Although the ‘back-end loaded’ cash flow profile can exacerbate financeability problems, companies may be able to mitigate the mismatch between indexed revenues and nominal financing costs by issuing inflation-indexed debt and/or entering into inflation swaps. The ability to issue these instruments varies across national capital markets. Furthermore, such back-end loaded profiles may be attractive to the class of investors that look to hedge against long-dated inflation-linked liabilities. For example, pension funds have become more prominent as investors in utilities regulated under a real WACC, indexed RAB model.
Second, tax
The price control packages must also provide companies with sufficient revenue to meet their corporation tax liabilities. In the UK, this is paid on profits at a (statutory) rate of 30% after interest payments. Again, there are two approaches. The first is the ‘tax wedge’. Here, the cost of equity—that is, the return required by equity investors—is multiplied by a ‘wedge’. This converts the post-tax cost of equity, sufficient to meet the requirements of equity investors, to a pre-tax cost of equity. When this value is applied to the RAB, it provides sufficient revenues to meet the tax liabilities. After tax payments are made, it still provides sufficient returns to satisfy equity investors.
Alternatively, some regulators prefer to use a ‘vanilla’ WACC. Here, the post-tax cost of equity is untouched. Instead, the assessment of likely corporation tax liabilities for a regulated company is managed as a cash-flow item and added to the operating costs of a business.
The box below provides more detail on these calculations and their underlying formulae.
Approaches to tax in setting the WACC
The formula for the pre-tax cost of capital is:
WACC (pre-tax) = g × Rd + 1/(1 – t) × Re × (1 – g)
where g is gearing; Rd is the cost of debt; Re the post-tax cost of equity; and t is the corporation tax rate.
This can be compared with the vanilla WACC, so called as it abstracts from all considerations of tax:
WACC (vanilla) = g × Rd + Re (1 – g)
The difference is the factor 1/(1 – t) applied to the cost of equity in the first calculation but not in the second. This factor (the tax wedge) is equal to approximately 1.42 at the UK statutory corporation tax rate of 30%. When the tax wedge is not applied (i.e. a vanilla WACC is used), it is necessary to fund the tax liabilities as part of the efficient operating costs of the business. Further complicating the issue is the post-tax WACC given by the formula:
WACC (post-tax) = g × Rd × (1 – t) + Re (1 – g)
This formula captures the tax benefit associated with gearing up (as interest is deducted before tax is calculated). However, as interest payable on debt is already factored into taxable profit, this calculation should not be used in the determination of prices.
What factors determine which approach to take?
The first point to note is that, actually, both approaches can be made equivalent. If detailed tax modelling is undertaken to estimate what the tax liability of a company will be during the price control period, a tax wedge to the post-tax cost of equity figure can be calculated, providing a revenue stream with the same net present value (NPV) as the NPV of the tax costs.
However, the equivalence breaks down if precise liabilities are not calculated—indeed, in using a tax wedge, it is more common for a standard corporation tax rate of 30% to be applied. There are often good reasons for this approach, not least of which is the simplicity it introduces to the regulatory price-setting formula. Nonetheless, over any five-year period, the effective tax rate of the company in question can differ from the statutory rate. This can lead to companies being either under- or over-remunerated for their tax liabilities.
Furthermore, in multi-company sectors, more problems can be created by using more than one generic figure. If a generic 30% tax wedge is used, it is often accompanied by another assumption—an industry-wide gearing figure. In other words, a pre-tax cost of capital is calculated to give sufficient revenues to meet the tax liabilities of a company taxed at 30% with, for example, 50% gearing.
Even within a five-year period, this creates an incentive on the regulated company to raise its gearing levels above 50% to increase the benefit of the interest tax shield and therefore reduce its tax bill relative to that assumed by the regulator (assuming that the costs of financial distress do not increase). However, the incentive becomes even stronger when it is likely that the gearing assumption will not only stay fixed for a five-year period, but indeed might not change very much thereafter.
The use of a vanilla WACC can help eliminate that incentive. It allows a split between the gearing assumption used in the WACC calculation and that used to calculate tax. So once a tax allowance is set, there is still an incentive for a company to gear up over the five-year period. But at the end of that period, the tax calculation at the next review can take account of the new higher gearing level without reference to a sector-wide gearing assumption.
Do they all give the same answer?
This article has so far considered the reasons for a regulator choosing to adopt either a nominal or real WACC, expressed on either a pre-tax or vanilla basis. As mentioned above, it is often considered that, at least in the long run, the balance between investor returns and consumers will be the same for each approach. In other words, it is argued that all approaches should provide the same NPV of cash flows to investors.
Nominal and real WACCs in a pre-tax world
Yet is this really the case? One reason to think that it may not be is that it is not clear which is the appropriate approach to calculating a particular real pre-tax cost of capital consistent with a nominal equivalent.
Consider the example in Table 1 taken from Ofcom’s recent determination on the cost of capital for BT’s copper access network, which led to a nominal pre-tax cost of capital of close to 10%.
Table 1 Ofcom’s parameter estimates for BT’s copper access WACC
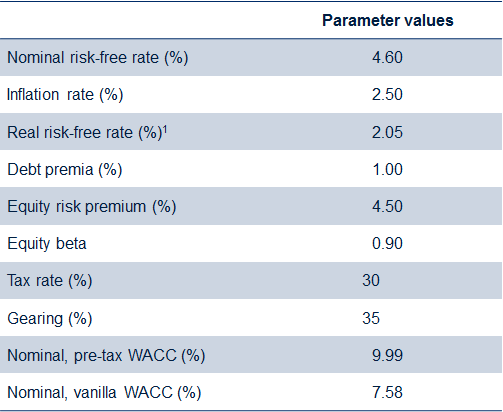
Source: Ofcom (2005), ‘Ofcom’s Approach to Risk in the Assessment of the Cost of Capital’, August.
What is the real pre-tax WACC equivalent of the 9.99% pre-tax nominal WACC? One option, taken by many regulators,4 would be to follow exactly the same building-block approach as used in the example above, but use the real risk-free rate estimate of 2.05%. This approach yields a real pre-tax estimate of 6.73%. However, an alternative approach, adopted on occasion by Ofcom, would be to take the outturn nominal pre-tax WACC of 9.99% calculated in Table 1 and use the Fisher relationship (see note to table) to derive the real equivalent. This yields a real pre-tax WACC of 7.31%.
In the first case, a regulator taking this approach to estimating the real pre-tax WACC would be adjusting for inflation by using a real rather than a nominal risk-free rate, and would then make an adjustment for tax in the cost of equity calculation.
The alternative approach would have the tax wedge applied to the cost of equity with a nominal risk-free rate. The adjustment for inflation is then made only at the end. It is clear that the sequence in which tax and inflation are dealt with can make a significant difference: in the numerical example above, the real pre-tax WACC changes by almost 60 basis points.
So, which is the ‘correct’ answer? If it was thought that the answer should be given by the approach that ensures that the NPV of cash flows received by investors is exactly equal to the cost of that investment, it appears that the answer is likely to be … neither! This can be demonstrated with the example of a simple regulatory financial model, where the following assumptions are made:
Over the years, a few sharp-eyed readers have pointed out that this conclusion is incorrect. In fact, there is a ‘correct’ answer—i.e. the ‘alternative’ approach described above. This is because tax is calculated based on nominal rather than real earnings, and therefore tax adjustments must be performed to the nominal, rather than the real, WACC.
- an initial investment of £1,000 is made in year 0, financed, as in the WACC calculation in Table 1, by 35% debt and 65% equity;
- the investment is depreciated over ten years;
- it is assumed that all cash flows (both costs and revenues) arise at the same time, on one particular day within that year;
- it is assumed that corporation tax of 30% is charged on profits, after the deduction of accounting depreciation, or capital allowances, which are calculated on a straight-line nominal basis, and interest payments, assuming that the debt attracts a nominal coupon; and
- £35 of debt is repaid every year, so that by the end of the period the asset value and debt position are nil.
Using these assumptions, the cash flows available to investors can be calculated as the sum of regulatory depreciation and allowed return, less corporation tax. As these are nominal, post-tax cash flows, it is appropriate to discount them using the nominal vanilla WACC of 7.58%.
Table 2 sets out the application of these assumptions in the case where a nominal pre-tax WACC of 9.99% is used, and therefore the RAB is not indexed by RPI.
Table 2 Calculation of cash flows to investors using nominal WACC (£)
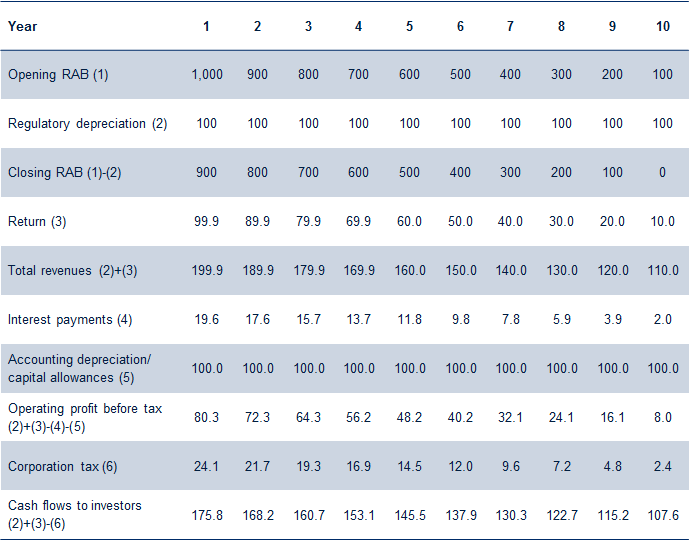
The NPV of these cash flows to investors is precisely £1,000—exactly the value of the initial investment.
This can be contrasted with the situation in which the RAB is indexed by inflation and a real pre-tax WACC, of either 6.73% or 7.31%, is used. The full cash-flow position is not set out here in as much detail as provided in Table 2, although the logic of the calculations is the same, simply with a different approach to calculating the total revenue line. The results are presented in Table 3.
The results presented in Table 3 are sensitive to the modelling approach—in particular, whether the regulatory allowed return (estimated WACC) is applied to the opening RAB or the average RAB, and the intra-year timing of the inclusion of the annual inflation adjustment to the RAB. It can be shown that the NPV of cash flows in the second row is within 0.1% of the initial investment—rather than the 5% indicated—which is consistent with there being a single correct approach of applying the tax adjustment to nominal parameters.
Table 3 Comparison of the impact on cash flows of nominal and real pre-tax WACCs
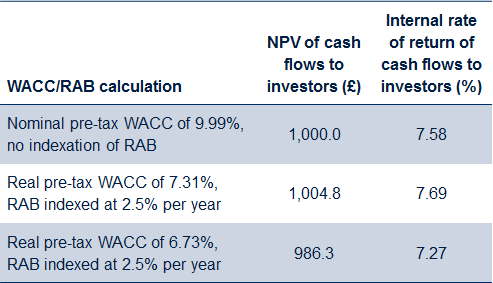
Compared with the nominal pre-tax approach, the higher real (alleged) equivalent leads to over-recovery. By contrast, the lower value actually leads to under-recovery. Further analysis can show that what really matters is the profile of the use of capital allowances/accounting depreciation relative to the regulatory depreciation allowance. In particular, the nominal WACC approach leads to precisely the ‘correct’ recovery of revenues because the profiles of regulatory depreciation and accounting depreciation are identical. By contrast, in situations where the accounting depreciation/profile of capital allowance is front-end loaded relative to the regulatory depreciation approach—which, given existing UK regulatory and tax accounting treatment precedent, is the more likely situation—it can be shown that it will always be the case that one of the pre-tax real estimates will lead to over-recovery and the other to under-recovery.5
In light of this, what should be the appropriate response from regulators? If they wish to continue to use the real pre-tax approach, it appears that some element of judgement—in addition to that required to derive each of the individual parameters—will be needed. Statements from regulators such as:
Ofcom believes that the costs associated with setting too low a cost of capital are greater than those associated with setting it too high6
may therefore point in the direction of using the higher of the two pre-tax real numbers, and hence, for some regulators, a policy change.
However, a different means for approaching the WACC could be considered. As seen above, these assumptions, and using the nominal pre-tax approach, appear to provide for cash flows that exactly offset the initial investment. Alternatively, in DPCR4, Ofgem switched from a pre-tax to a vanilla approach. As such, the next section considers how this analysis fits into the vanilla WACC framework.
Nominal and real WACC in a vanilla world
Using exactly the same individual parameter values as set out in Table 1, it is possible to derive the vanilla WACC estimates in Table 4.
Table 4 Different vanilla WACC estimates (%)

There is one key point to note here. In contrast to the pre-tax calculations, the vanilla framework reverses the effect of the different approaches. The approach favoured by Ofcom now leads to a lower figure than that favoured by other regulators. That is, using a nominal risk-free rate and adjusting for inflation after the nominal WACC has been calculated now leads to a lower value than using a real risk-free rate to derive a real WACC. Mathematically, this is a consequence of the fact that the multiplicative effect of the tax wedge is no longer factored into the calculations.
The cash flows and internal rates of return (IRRs) that result from this alternative approach can be calculated in much the same way as before. The results are presented in Table 5.
Table 5 Comparison of the impact on cash flows of nominal and real vanilla WACCs
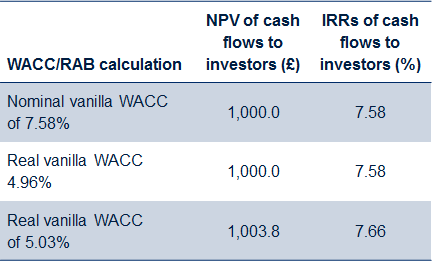
As before, the nominal vanilla approach provides for an NPV of revenues exactly offsetting the initial investment.
However, in contrast to the pre-tax results, the ‘Ofcom’ approach to setting the real vanilla WACC also achieves the same result. Only one approach ‘fails’—building up from a real risk-free rate calculation. In contrast to the pre-tax outcome, in this context it actually creates a slight over-recovery.
As indicated in the balloons above, this is not a surprising result. Applying tax adjustments to the nominal rather than real WACC is the correct approach to converting between the vanilla and pre-tax WACC.
Conclusions
The choice of how to adjust for tax and inflation within the regulatory price-setting formula is complex, and can have a variety of impacts on the regulated company. These may include the extent to which the price control package is ‘financeable’ and the incentives on the capital structure of the firm. However, in addition to many of these issues that have traditionally been considered relevant by UK regulators, it appears that the extent to which investors will under- or over-recover their investment must also be factored into this analysis.
1 Ofgem (2004), ‘Electricity Distribution Price Control Review: Final Proposals’, November; and Network Rail (2003), ‘Response to Third Consultation Paper’, September.
2 There is a concern that investors are being required to invest in companies whose current cash-flow position is relatively fragile, with the prospect of the return on their investment being generated a long way into the future.
3 Currie, D. (2003), ‘Mutualisation and Debt Only Vehicles’, Competition and Regulation, Institute of Economic Affairs.
4 For example, the Competition Commission, Ofgem (when it has used a pre-tax WACC), the Civil Aviation Authority, and the Office of Rail Regulation.
5 Davies, K. (undated), ‘Access Regime Design and Required Rates of Return: Pitfalls in Adjusting for Inflation and Tax Effects’, working paper.
6 Ofcom (2005), ‘Ofcom’s Approach to Risk in the Assessment of the Cost of Capital’, January.
Download
Related

Time to get real about hydrogen (and the regulatory tools to do so)
It’s ‘time for a reality check’ on the realistic prospects of progress towards the EU’s ambitious hydrogen goals, according to the European Court of Auditors’ (ECA) evaluation of the EU’s renewable hydrogen strategy.1 The same message is echoed in some recent assessments within member states, for example by… Read More

Financing the green transition: can private capital bridge the gap?
The green transition isn’t just about switching from fossil fuels to renewable or zero-carbon sources—it also requires smarter, more efficient use of energy. By harnessing technology, improving energy efficiency, and generating power closer to where it’s consumed, we can cut both costs and carbon emissions. In this episode of Top… Read More

