Investing, insurance or gambling?
The distinction between investment, insurance and gambling is an essential one for policymakers and regulators. At the most basic level it is easy to see the differences between these products. But is it possible to extend the theoretical distinctions to more complex products and so give consumers clearer guidance? Fod Barnes, Senior Adviser at the UK Payment Systems Regulator, and previously a Senior Adviser at Oxera, explores the issues.
This article was first published on the UK Financial Conduct Authority’s (FCA) Insight thought leadership webpages at https://www.fca.org.uk/insight/investing-insurance-or-gambling. It does not necessarily represent the views of the FCA.
Professionals in financial markets are used to the sneers—‘It’s all just gambling’. It may be an unfair smear (mostly), and often it is easy to distinguish between a ‘flutter’ and an investment, or even an insurance policy.
But while it may be easy in practice to distinguish between gambling and certain financial transactions, it is far harder to do in theory. And in this case, theory matters, for whether an activity is classified as buying a financial product or as gambling will determine its status in law and in regulation, and is sure to influence the attitudes of consumers who are considering whether or not to hand over their money.
The solution may lie in trying to make these distinctions, not by trying to define the product, but by considering the typical outcomes.
Rather than asking what the product is supposed to be, we could ask: what happens to people who buy these things?
Let us start by looking at three relatively pure examples of investing, insurance and gambling. Buying £100 worth of a FTSE 100 tracker fund is clearly investing. Buying a betting slip for £100 from a bookmaker, with the payout dependent on Spring Beauty finishing first in the 2.30pm handicap stakes at Chepstow, is clearly gambling. And paying £100 to an insurance company that pays out the cost of accidental or criminal damage to your property is clearly buying insurance.
So far, so easy
But while intuitively very different, all three of these have core features in common. They all involve making a payment of £100 right now, for a product that may deliver a payout in the future, subject to certain conditions being met. (The value of the FTSE 100 in the future; the results of a horse race; and the occurrence of theft or fire at your house.) At the time the purchase is made, it is not known for certain what the payout will be or whether a payout will be made at all.
So what are the differences? These are clearest (indeed, they are utterly stark) when we look at the outcome distributions—what happens to people when they buy these products.
The outcome distributions for these basic products can be theoretically modelled by showing the outcomes for 100 typical consumers who spend £100 on each product, and comparing them with another 100 people who don’t buy the product and simply keep their cash under the mattress. (The detailed assumptions used for these models can be found in the box below. They are, I hope, uncontroversial.)
A note on method
The graphs in this article are based on a model of 100 customers. The customers either spend £100 (on buying an investment product, insuring their house or betting on their favourite horse) or they keep the £100 under the mattress (the counterfactual). The positions of the customers are compared after (in this case) an arbitrary year. The assumptions are as follows.
Investing
The average (net) annual return is 5%, subject to a random multiplier that is normally distributed about 1.05 (5% return) and has a standard deviation of 0.13.
Insurance
The costs of running the insurance company are assumed to be 10% of premiums, so 90% of total premium income is paid out in compensation; 5% of customers experience a loss, varying from £5,000 to £200, for which they are compensated.
Gambling
The cost of running the bookmaker is assumed to be 5% of the money wagered. So 95% of what is wagered is paid out as winnings. 10% of bets win, and the decimal odds at which they win vary from 1.2 to 20.
If we present these models graphically, looking at the distribution of outcomes and also the average outcomes, the differences between investment, insurance and gambling are glaring.
Figure 1 Investment
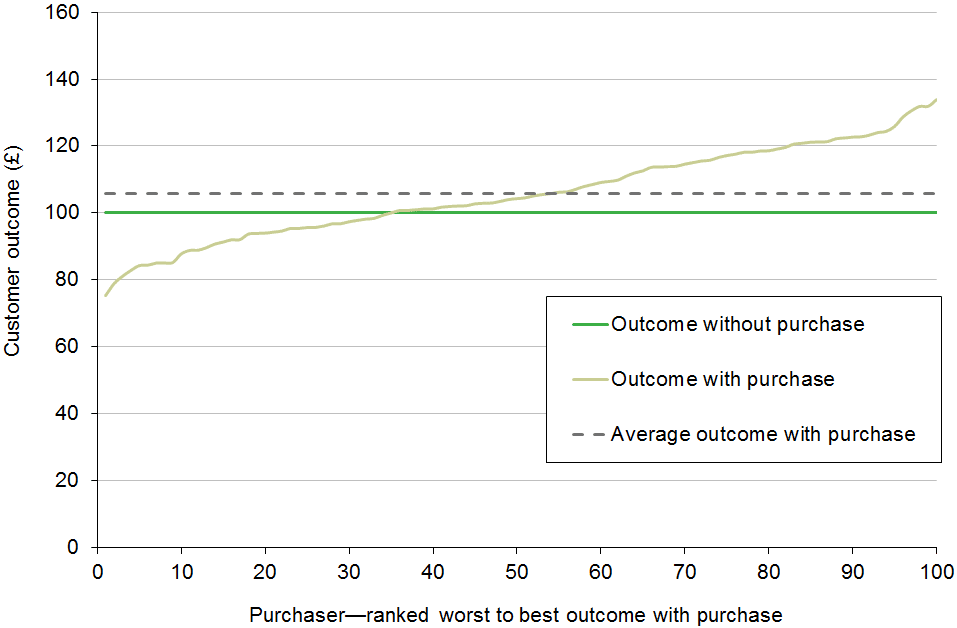
Figure 2 Gambling
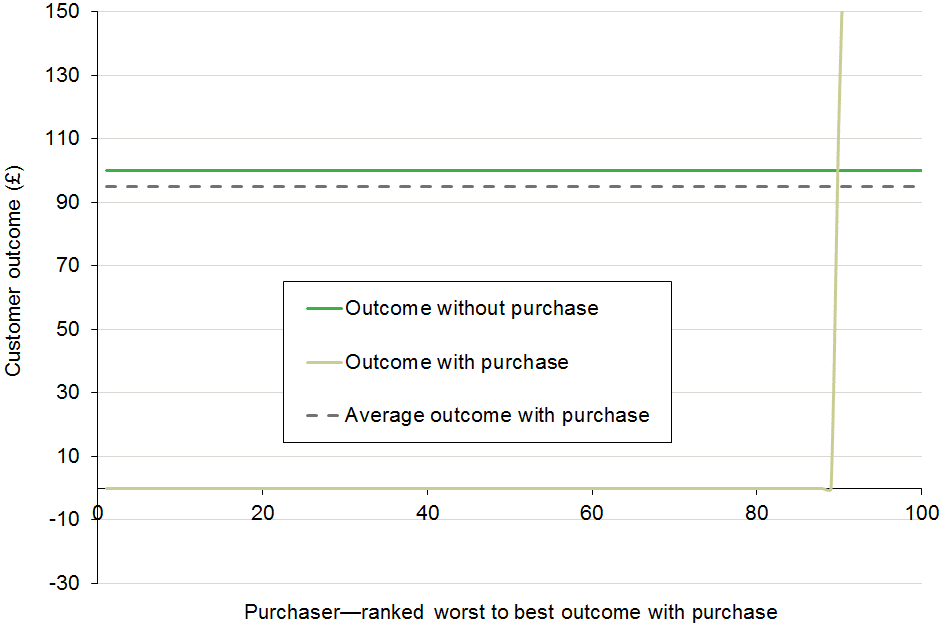
Source: Fod Barnes.
Figure 3 Insurance

Source: Fod Barnes.
The two key metrics here are the average outcome of buying or not buying the product, and the majority outcome—what happens to most people who either do or do not buy.
For investment products, the vast majority of those who buy the product (invest) do better than those who don’t. And the average outcome for those who invest is also better than for those who don’t.
For both insurance and gambling, those who do buy the products (those who do bet and who do take out insurance) on average lose money in comparison with those who don’t. The crucial phrase here, of course, is ‘on average’. This creates a clean distinction in typical outcomes between investment on the one hand and insurance and gambling on the other.
Gambling and insurance are similar in that most people who gamble or buy insurance on average lose money. But as the figures above illustrate, the outcome is quite different in one key respect: insurance narrows the range of outcomes, while gambling widens it.
For insurance products, most people are better off if they do not buy insurance—they save the premium, and their house does not burn down. But a small number of these uninsured people are catastrophically worse off—their house burns down and they have no insurance cover. So, among the uninsured we have a wide range of outcomes. The effect of buying insurance is to narrow this range. Most insurance buyers suffer a small cost (paying the premium), but no-one who has bought insurance suffers a catastrophic loss.
Now consider gambling. All those who refrain from gambling have exactly the same outcome: they lose nothing and they gain nothing. This is the ultimate narrow range of outcomes.
The effect of gambling is to widen the outcomes. Among those who place a bet, the vast majority are worse off (they lose their stake), but a very small number make a big profit as their horse romps home.
Of course, insurance premiums are not a pure loss as the payer does gain peace of mind in return. Similarly, the gambler may argue that while they typically lose, the activity of gambling still gives them pleasure. However, neither of these points alters the significance of the outcome distribution model, which captures financial outcomes of these products.
With these metrics in mind for investment, insurance and gambling in their purest forms, we can construct the table below.
Table 1 Returns and outcomes
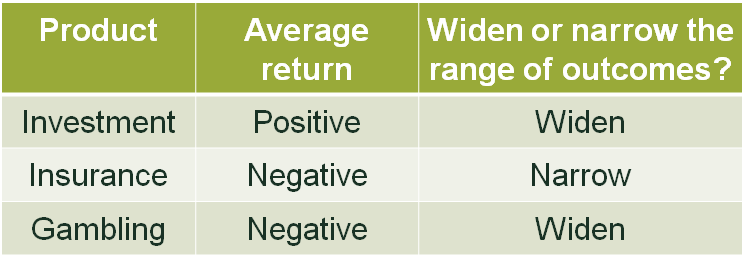
So far, I have considered investment, insurance and gambling in quite pure forms—a FTSE tracker, general insurance, and a flutter on the horses. And, of course, the outcome distribution model I have described has in these cases served only to confirm what we already intuitively knew—that investment, insurance and gambling are very different things.
But having established this perspective, I would suggest that any real or proposed financial product can and should be considered on the basis of this matrix. What is more, we can consider not just individual products in this way, but combinations of products. And, going the final step, we can take a rounded view not of whether a particular product is gambling or investing, but of whether the combined activities of a particular consumer are gambling or investing.
A single product may not tell the whole story
In theory, an insurance policy could be made to deliver the same outcome distribution as gambling if, for example, I were able to insure my neighbour’s house against fire. The typical outcome for people who insured their neighbours house would be a loss—they pay the premium but their neighbour’s house does not burn down. But for a small number of people this would turn into a windfall—their neighbour’s house burns down and they (not their neighbour) collect a big payout. This of course is why there are very tight regulatory and legal restrictions designed to stop the use of insurance contracts in this way.
But the crucial point is that turning an insurance policy into gambling depends not on the structure of the policy itself, but on other characteristics or investments of the consumer. In this case: do they own the house that is insured? (Or, in the jargon, do they have an ‘insurable interest’?)
While regulation is in place that stops people using insurance in the way described above—as a gambling product—there are other financial products which are not covered by such restrictions and which all too often are used in ways that demonstrate the same distribution of outcomes as gambling.
One such product is a contract for difference (CFD). A CFD can be used as insurance: an investor who has bought a FTSE 100 tracker may also take out a CFD, which will pay out if the FTSE crashes. The average return on their CFD will be negative—it’s a cost that will not lead to a payout. But among FTSE 100 investors who buy an appropriate CFD, there will be a narrower range of outcomes, and none of them will suffer a major loss from a market crash. In other words, for investors who buy a tracker and hedge it with a CFD, the CFD looks very like insurance.
But purchased on its own by someone with no investment in a FTSE 100 tracker, the same CFD may exhibit the exact opposite characteristics. On average and for most of these buyers, it will lead to a loss—the cost of the CFD. But for a small proportion of people for whom events and timing coincide, the CFD will deliver a big windfall. In other words, the distribution of outcomes looks like a gambling product.
So, the same product can look like insurance or gambling, not because of any change in the product itself, but because of the other products held by the consumer.
The gambling features of CFDs are borne out by research. Analysis of various regulators worldwide has shown that around 80% of retail buyers of CFDs make losses, and on average they lose in the order of £2,000 each per year.1
Is this a sign of massive gambling losses, or should we regard these as the premiums paid by cautious investors taking out insurance? The answer is that we simply cannot know without first knowing whether these CFD buyers also held other offsetting investments.
And so it is that regulators and legislators have faced a conundrum in defining CFDs, and a number of other products, whose distribution of outcomes look like insurance in one situation and like gambling in another.
To date, regulators have given these products the benefit of the doubt. Products which can be used as investments or insurance are defined as such.
But perhaps regulators, and indeed legislators, need to consider how these products are used in practice and to consider introducing definitions that take this into account. This approach has been reflected in recent FCA rules on CFDs, for example, but could regulators go further and give more explicit guidance to consumers by using blunter terms?
Warning: explicit language
Based on the matrix I have outlined here, one could say that investors who buy derivatives, including options, futures, CFDs or binaries on individual equities or commodities, but who own no offsetting assets, are categorically not investing. They are gambling. Should regulators be saying this explicitly to consumers, or requiring firms to do so?
It is also possible to extend this approach and apply the distributional outcomes model to a huge range of behaviours in finance. For example, day trading (even on equities) has an outcomes distribution that looks like gambling. Once the transaction costs are taken into account, the average outcome for day trading (and the experience of the majority of day traders) is a net loss, while only a small number make a profit.
Similarly, trading in foreign currencies, bitcoin and other ‘cryptocurrencies’, when considered through this outcome distribution approach, also exhibits the characteristics not of investing, but of gambling.
It is clear that the current assumption that products can be classified as investment, insurance or gambling by trying to define some theoretical ‘essence of the product’ is not useful or even possible. The same may also be the case for crudely defining a product as ‘high-risk’ or ‘low-risk’.
Modelling outcome distribution for products or combinations of products would provide far better answers to these questions.
It could also provide regulators with some standard tools to assess the products that financial firms are selling and to provide consumers with a more meaningful explanation of what they are buying.
1 Financial Conduct Authority (2016), ‘Enhancing conduct of business rules for firms providing contract for difference products to retail clients’, consultation paper CP16/40, December, para. 1.5.
Download
Contact

Matthew Johnson
PartnerGuest author
Fod Barnes
Senior Adviser, UK Payment Systems Regulator
Contributor
Related
Download
Related

Economics of the Data Act: part 1
As electronic sensors, processing power and storage have become cheaper, a growing number of connected IoT (internet of things) devices are collecting and processing data in our homes and businesses. The purpose of the EU’s Data Act is to define the rights to access and use data generated by… Read More

Adding value with a portfolio approach to funding reduction
Budgets for capital projects are coming under pressure as funding is not being maintained in real price terms. The response from portfolio managers has been to cancel or postpone future projects or slow the pace of ongoing projects. If this is undertaken on an individual project level, it could lead… Read More
